题目内容
设曲线C:![]() 的离心率为
的离心率为![]() ,右准线
,右准线![]() 与两渐近线交于P,Q两点,其右焦点为F,且△PQF为等边三角形。
与两渐近线交于P,Q两点,其右焦点为F,且△PQF为等边三角形。
(1)求双曲线C的离心率![]() ;
;
(2)若双曲线C被直线![]() 截得弦长为
截得弦长为![]() ,求双曲线方程;
,求双曲线方程;
(3)设双曲线C经过![]() ,以F为左焦点,为
,以F为左焦点,为![]() 左准线的椭圆的短轴端点为B,求BF 中点的轨迹N方程。
左准线的椭圆的短轴端点为B,求BF 中点的轨迹N方程。
(1)2
(2)![]() 或
或![]()
(3)![]()
![]() (或
(或![]() )
)
解析:
⑴如图:易得P![]()
设右准线![]() 与
与![]() 轴的交点为M,
轴的交点为M,
∵△PQF为等边三角形
∴|MF|=![]() |PM|
|PM|
∴![]()
化简得:![]()
∴![]()
∴![]()
⑵ 由⑴知:![]()
∴双曲线方程可化为:![]() ,即
,即![]()
联列方程: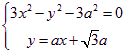
消去![]() 得:
得:![]()
由题意: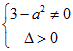 (*)
(*)
设两交点A![]() ,B
,B![]()
则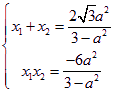
∴|AB|=![]() =
=![]()
化简得:![]() ,即
,即![]()
解得:![]() 或
或![]() ,均满足(*)式
,均满足(*)式
∴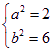 或
或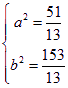
∴所求双曲线方程为:![]() 或
或![]()
⑶由⑴知双曲线C可设为:![]()
∵其过点A![]() ∴
∴![]()
∴双曲线C为:![]()
∴其右焦点F![]() ,右准线
,右准线![]() :
:![]()
设BF的中点N![]() ,则B
,则B![]()
由椭圆定义得:![]() (其中
(其中![]() 为点B到
为点B到![]() 的距离)
的距离)
∴![]()
化简得:![]()
∵点B是椭圆的短轴端点,故![]()
∴BF的中点的轨迹方程是:![]()
![]() (或
(或![]() )
)

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目