题目内容
如图所示，在四棱锥P―ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．
(1)证明：PA∥平面EDB；
(2)求EB与底面ABCD所成角的正切值．
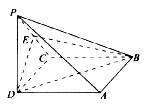
解：(1)如图所示建立空间直角坐标系，D为坐标原点，设DC=
，连接AC交BD于G，
连接EG，依题意得A(，0，0)、P(0，0，)、E(0，
，)．
∵底面ABCD是正方形，∴G是此正方形的中心，故点G的坐标为(，，0)，
∴
∴
，
这表明PA∥EG，而EG
平面EDB，且PA
平面EDB，
∴PA//平面EDB．
(2)由题意得
=(，，
)，又PD⊥面ABCD，则
为其法向量．
又 (0，0，1)．∴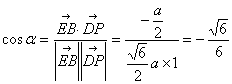
，
又所求角应小于90°，即
，则
，
∴
，
∴所求角即
的余角的正切值为
．
练习册系列答案
相关题目
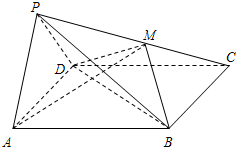如图所示，在四棱锥P-ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABCD是边长为2的菱形，∠BAD=60°，M为PC上一点，且PA∥平面BDM．
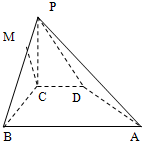如图所示，在四棱锥P-ABCD中，PC⊥平面ABCD，PC=2，在四边形ABCD中，∠B=∠C=90°，AB=4，CD=1，点M在PB上，PB=4PM，PB与平面ABCD成30°的角．
（2012•广东）如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．
如图所示，在四棱锥P-ABCD中，底面四边形ABCD是正方形，PD⊥平面ABCD，E为PC的中点．
如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AD=2AB=2，M为PD上的点，若PD⊥平面MAB