题目内容
已知抛物线的顶点在坐标原点,焦点为 ,点
,点 是点
是点 关于
关于 轴的对称点,过点
轴的对称点,过点 的直线交抛物线于
的直线交抛物线于 两点。
两点。
(Ⅰ)试问在 轴上是否存在不同于点
轴上是否存在不同于点 的一点
的一点 ,使得
,使得 与
与 轴所在的直线所成的锐角相等,若存在,求出定点
轴所在的直线所成的锐角相等,若存在,求出定点 的坐标,若不存在说明理由。
的坐标,若不存在说明理由。
(Ⅱ)若 的面积为
的面积为 ,求向量
,求向量 的夹角;
的夹角;
【答案】
(Ⅰ)存在T(1,0);(Ⅱ)向量 的夹角
的夹角 .
.
【解析】
试题分析:(Ⅰ)试问在 轴上是否存在不同于点
轴上是否存在不同于点 的一点
的一点 ,使得
,使得 与
与 轴所在的直线所成的锐角相等,若存在,求出定点
轴所在的直线所成的锐角相等,若存在,求出定点 的坐标,若不存在说明理由,这是一个探索性命题,解这一类问题,一般都假设其存在,若能求出
的坐标,若不存在说明理由,这是一个探索性命题,解这一类问题,一般都假设其存在,若能求出 的坐标,就存在这样的点,若不能求出
的坐标,就存在这样的点,若不能求出 的坐标,就不存在这样的点,本题假设存在
的坐标,就不存在这样的点,本题假设存在 满足题意,
满足题意, 与
与 轴所在的直线所成的锐角相等,则它们的斜率互为相反数,结合直线与抛物线的位置关系,采用设而不求的方法即可解决;(Ⅱ)求向量
轴所在的直线所成的锐角相等,则它们的斜率互为相反数,结合直线与抛物线的位置关系,采用设而不求的方法即可解决;(Ⅱ)求向量 的夹角,可根据夹角公式
的夹角,可根据夹角公式 ,分别求出
,分别求出 ,与
,与 即可.
即可.
试题解析:(Ⅰ)由题意知:抛物线方程为: 且
且
设 直线
直线 代入
代入 得
得
 ,
,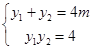
假设存在 满足题意,则
满足题意,则





 存在T(1,0)
存在T(1,0)
(Ⅱ) ,
,




 (13分)
(13分)
考点:直线与抛物线位置关系,向量夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐