题目内容
在极坐标系中，圆p=2上的点到直线p（cosθ+| 3 |
分析：圆p=2、直线p（cosθ+
sinθ）=6化为直角坐标方程，求出圆心到直线的距离，再求圆p=2上的点到直线p（cosθ+
sinθ）=6的距离的最小值．
| 3 |
| 3 |
解答：解：圆p=2、直线p（cosθ+
sinθ）=6化为直角坐标方程，
分别为x2+y2=4，x+
y-6=0
圆心到直线的距离为：
=3
所以圆p=2上的点到直线p（cosθ+
sinθ）=6的距离的最小值是3-2=1
故答案为：1
| 3 |
分别为x2+y2=4，x+
| 3 |
圆心到直线的距离为：
| |-6| | ||||
|
所以圆p=2上的点到直线p（cosθ+
| 3 |
故答案为：1
点评：本题考查点到直线的距离公式，简单曲线的极坐标方程和直角坐标方程的互化，考查计算能力，是基础题．
练习册系列答案
口算题天天练系列答案
相关题目
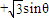）=6的距离的最小值是 ．
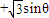）=6的距离的最小值是 ．