题目内容
已知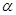 、
、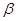 是不同的两个平面,直线
是不同的两个平面,直线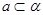 ,直线
,直线 ,命题
,命题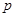 :
: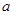 与
与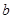 无公共点;命题
无公共点;命题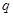 :
: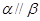 , 则
, 则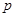 是
是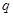 的 条件.
的 条件.
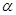 、
、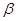 是不同的两个平面,直线
是不同的两个平面,直线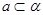 ,直线
,直线 ,命题
,命题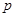 :
: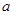 与
与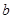 无公共点;命题
无公共点;命题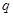 :
: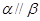 , 则
, 则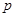 是
是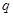 的 条件.
的 条件.必要非充分;
试题分析:已知
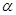 、
、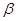 是不同的两个平面,直线
是不同的两个平面,直线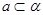 ,直线
,直线 ,
,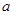 与
与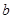 无公共点,无法推出
无公共点,无法推出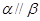 ;而
;而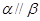 可推出
可推出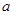 与
与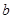 无公共点,所以
无公共点,所以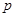 是
是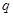 的必要非充分条件.
的必要非充分条件.点评:基础题,充要条件的判断问题,是高考不可少的内容,特别是充要条件可以和任何知识点相结合。充要条件的判断一般有三种思路:定义法、等价关系转化法、集合关系法。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
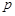
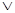
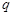 是假命题”是“
是假命题”是“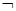
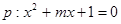 有两个不等的负根,
有两个不等的负根,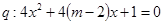 无实数根,若p或q为真,p且q为假,求m的取值范围。
无实数根,若p或q为真,p且q为假,求m的取值范围。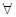
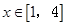 时,
时,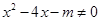 ”是假命题,则
”是假命题,则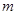 的取值范围( )
的取值范围( )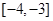
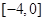
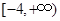
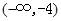
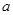 、
、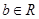 ,若
,若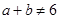 ,则
,则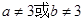 ”是一个假命题
”是一个假命题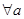 、
、 ”的否定是:
”的否定是: 、
、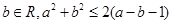 ”
”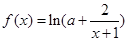 的图象关于原点对称,则
的图象关于原点对称,则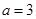
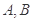 满足
满足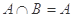 则
则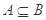 ;
;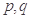 ,若
,若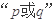 为真,则
为真,则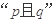 为真;
为真;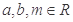 ,若
,若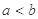 ,则
,则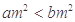 ;
;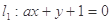 与直线
与直线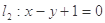 垂直,则
垂直,则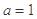 .
.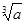 >
>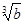 >0”的逆否命题
>0”的逆否命题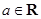 ,则“
,则“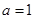 ”是“
”是“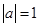 ”的( )条件( )
”的( )条件( )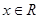 ,使得
,使得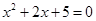 ”的否定是 .
”的否定是 .