题目内容
某高中食堂定期购买面粉.已知学校食堂每天早餐需用面粉600公斤,每公斤面粉的价格为5元,而面粉的保管等其它费用为平均每百公斤每天3元,购买面粉每次需支付运费900元,则学校食堂每隔 天购买一次面粉,才能使平均每天所支付的总费用最少,最少总费用为 元.
【答案】分析:每天所支付的费用是每x天购买粉的费用与保存面粉的费用及每次支付运费和的平均数,故可以设x天购买一次面粉,将平均数表示成x的函数,根据所得的函数的具体形式求其最小值即可.
解答:解:设该厂应每x天购买一次面粉,其购买量为600x公斤,由题意知,面粉的保管等其他费用为3[6x+6(x-1)+…+6×2+6×1]=9x(x+1).
设平均每天所支付的总费用为y1元,则y1=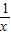 [9x(x+1)+900]+5×600
[9x(x+1)+900]+5×600
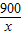 +9x+3009≥2
+9x+3009≥2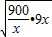 +3009=3189.
+3009=3189.
当且仅当9x=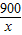 ,即x=10时取等号,
,即x=10时取等号,
即该厂应每10天购买一次面粉,才能使平均每天所支付的总费用最少,最少为3189元.
故答案为:10,3189.
点评:本题考点是函数模型的选择与应用,考查根据实际问题选择函数模型的能力,以及根据具体的函数模型求最值,属于中档题.
解答:解:设该厂应每x天购买一次面粉,其购买量为600x公斤,由题意知,面粉的保管等其他费用为3[6x+6(x-1)+…+6×2+6×1]=9x(x+1).
设平均每天所支付的总费用为y1元,则y1=
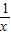 [9x(x+1)+900]+5×600
[9x(x+1)+900]+5×600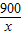 +9x+3009≥2
+9x+3009≥2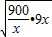 +3009=3189.
+3009=3189.当且仅当9x=
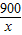 ,即x=10时取等号,
,即x=10时取等号,即该厂应每10天购买一次面粉,才能使平均每天所支付的总费用最少,最少为3189元.
故答案为:10,3189.
点评:本题考点是函数模型的选择与应用,考查根据实际问题选择函数模型的能力,以及根据具体的函数模型求最值,属于中档题.

练习册系列答案
相关题目