题目内容
定义:对于任意n∈N*,满足条件 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.(1)若an=-n2+9n(n∈N*),证明:数列an是T数列;
(2)设数列bn的通项为
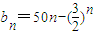 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围;(3)设数列
 (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.
【答案】分析:(1)由an=-n2+9n,得an+an+2-2an+1=-n2+9n-(n+2)2+9(n+2)+2(n+1)2-18(n+1)=-2,所以数列an满足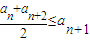 .由此能够证明数列an是T数列.
.由此能够证明数列an是T数列.
(2)因为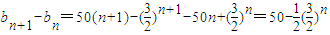 ,所以当
,所以当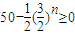 即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.
即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.
(3)当1<p≤2时,对于n∈N*有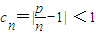 ,所以当
,所以当 时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.
时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.
解答:解:(1)由an=-n2+9n,得an+an+2-2an+1=-n2+9n-(n+2)2+9(n+2)+2(n+1)2-18(n+1)=-2
所以数列an满足 .(2分)
.(2分)
又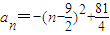 ,当n=4或5时,an取得最大值20,即an≤20.
,当n=4或5时,an取得最大值20,即an≤20.
综上,数列an是T数列.(4分)
(2)因为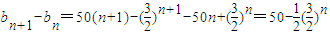 ,
,
所以当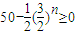 即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)
即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)
当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,
所以,M的取值范围是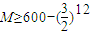 (9分)
(9分)
(3)①当1<p≤2时,当n=1时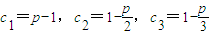 ,
,
由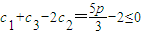 得
得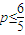 ,
,
即当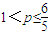 时符合
时符合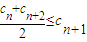 条件.(11分)
条件.(11分)
若n≥2,则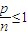 ,此时
,此时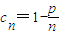
于是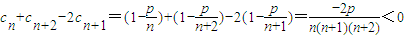
又对于n∈N*有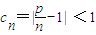 ,
,
所以当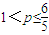 时数列cn是T数列;(13分)
时数列cn是T数列;(13分)
②当2<p≤3时,
取n=1则: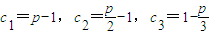 ,
,
由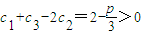 ,所以2<p≤3时数列cn不是T数列.(15分)
,所以2<p≤3时数列cn不是T数列.(15分)
③当p>3时,
取n=1则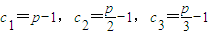 ,
,
由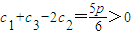 ,所以p>3时数列cn不是T数列.(17分)
,所以p>3时数列cn不是T数列.(17分)
综上:当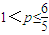 时数列cn是T数列;当
时数列cn是T数列;当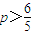 时数列cn不是T数列.(18分)
时数列cn不是T数列.(18分)
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
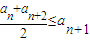 .由此能够证明数列an是T数列.
.由此能够证明数列an是T数列.(2)因为
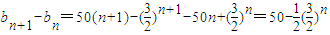 ,所以当
,所以当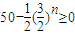 即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.
即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.(3)当1<p≤2时,对于n∈N*有
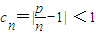 ,所以当
,所以当 时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.
时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.解答:解:(1)由an=-n2+9n,得an+an+2-2an+1=-n2+9n-(n+2)2+9(n+2)+2(n+1)2-18(n+1)=-2
所以数列an满足
 .(2分)
.(2分)又
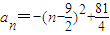 ,当n=4或5时,an取得最大值20,即an≤20.
,当n=4或5时,an取得最大值20,即an≤20.综上,数列an是T数列.(4分)
(2)因为
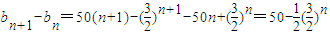 ,
,所以当
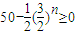 即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)
即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,
所以,M的取值范围是
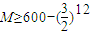 (9分)
(9分)(3)①当1<p≤2时,当n=1时
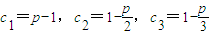 ,
,由
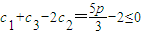 得
得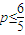 ,
,即当
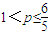 时符合
时符合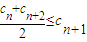 条件.(11分)
条件.(11分)若n≥2,则
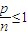 ,此时
,此时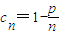
于是
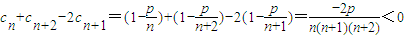
又对于n∈N*有
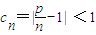 ,
,所以当
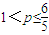 时数列cn是T数列;(13分)
时数列cn是T数列;(13分)②当2<p≤3时,
取n=1则:
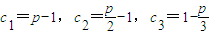 ,
,由
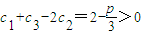 ,所以2<p≤3时数列cn不是T数列.(15分)
,所以2<p≤3时数列cn不是T数列.(15分)③当p>3时,
取n=1则
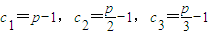 ,
,由
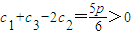 ,所以p>3时数列cn不是T数列.(17分)
,所以p>3时数列cn不是T数列.(17分)综上:当
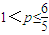 时数列cn是T数列;当
时数列cn是T数列;当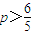 时数列cn不是T数列.(18分)
时数列cn不是T数列.(18分)点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
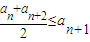 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.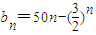 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由. 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列. ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.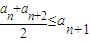 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.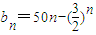 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围;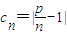 (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由. 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列. ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.