题目内容
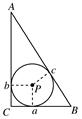
如图,若Rt△ABC的斜边AB=2,内切圆的半径为r,则r的最大值为
( )
( )

| A. | B.1 |
| C. | D.-1 |
D
先根据三角形内切圆的性质,用三边表示出内切圆的半径,进而根据均值不等式求得a+b的最大值,进而求的r的最大值.
解:∵r= =
=
∵4=a2+b2≥ ,
,
∴(a+b)2≤8.
∴a+b≤2 ,
,
∴r≤ -1.
-1.
故选D.
解:∵r=
 =
=
∵4=a2+b2≥
 ,
,∴(a+b)2≤8.
∴a+b≤2
 ,
,∴r≤
 -1.
-1.故选D.

练习册系列答案
相关题目
 、
、 都为正数,且
都为正数,且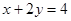 ,则lgx+lgy的最大值是
,则lgx+lgy的最大值是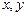 满足
满足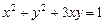 ,则
,则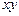 的最大值是_____ ___
的最大值是_____ ___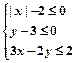 所表示的平面区域为
所表示的平面区域为 ,若
,若 、
、 为
为 |的最大值为
|的最大值为 的解集是 。
的解集是 。 路线走到同一地点。甲有一半时间以速度m行走,另一半时间以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走。如果m≠n,甲、乙两人走完这段路程所用的时间分别为t1,t2,则有
路线走到同一地点。甲有一半时间以速度m行走,另一半时间以速度n行走;乙有一半路程以速度m行走,另一半路程以速度n行走。如果m≠n,甲、乙两人走完这段路程所用的时间分别为t1,t2,则有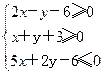 ,则
,则 的最大值为_____________.
的最大值为_____________.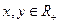 ,且
,且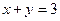 ,则
,则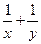 的最小值为 ( )
的最小值为 ( )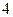
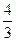
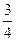
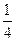

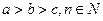 ,且
,且 恒成立,则
恒成立,则 的最大值是( )
的最大值是( )
 B
B C
C D
D