题目内容
已知函数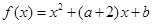 ,满足
,满足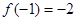 ;
;
(1)若方程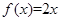 有唯一的解;求实数
有唯一的解;求实数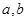 的值;
的值;
(2)若函数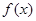 在区间
在区间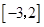 上不是单调函数,求实数
上不是单调函数,求实数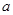 的取值范围。
的取值范围。
【答案】
(1)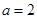 ,
,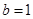 (2)
(2)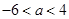
【解析】
试题分析:解(1)由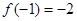 知,
知,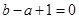 ①,又
①,又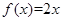 有唯一的解,故
有唯一的解,故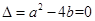 将①式代入上式得:,
将①式代入上式得:,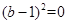 故
故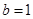 ,代入①得,
,代入①得,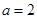 7分
7分
(2)因为函数 在区间
在区间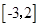 上不是单调函数,所以对称轴
上不是单调函数,所以对称轴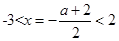 ,
,
解得: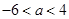 13分
13分
考点:函数与方程
点评:解决的关键是利用二次函数的性质以及函数单调性来解决,属于常规试题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ,满足
,满足 ,且
,且 ,
, .则
.则
 =.( )
=.( ) 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 时,
时, ,其中
,其中 .
. 上的解析式,并求出函数
上的解析式,并求出函数 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
).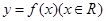 ,满足
,满足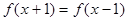 ,且
,且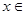 [
[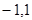 ],
],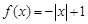 ,则
,则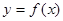 与
与 的图像的交点的个数为 ( )
的图像的交点的个数为 ( ) 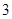 个 B.
个 B.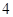 个 C.
个 C. 个
D.
个
D. 个
个