题目内容
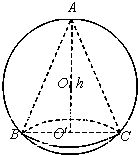
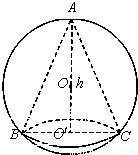
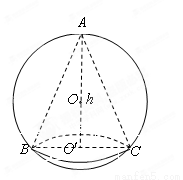
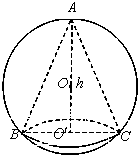 如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,
如图,已知球的半径为定值R,球内接圆锥的高为h(h>R),体积为V,(1)写出以h表示V的函数关系式V(h);
(2)当h为何值时,V(h)有最大值,并求出该最大值.
分析:(1)连接OC,设O′C=r,有OC=R,O′O=h-R,确定h与r的关系,即可以h表示V的函数关系式V(h);
(2)利用基本不等式,即可求最大值.
(2)利用基本不等式,即可求最大值.
解答: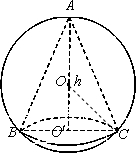 解:(1)连接OC,设O′C=r,有OC=R,O′O=h-R,
解:(1)连接OC,设O′C=r,有OC=R,O′O=h-R,
则有(h-R)2+r2=R2,即r2=2Rh-h2.
∴V(h)=
πr2h=
-
(R<h<2R)
(2)V(h)=
π(4R-2h)•h•h≤
•(
)3=
πR3
不等式取等号条件为4R-2h=h,即当h=
R时,V(h)有最大值
πR3.
 解:(1)连接OC,设O′C=r,有OC=R,O′O=h-R,
解:(1)连接OC,设O′C=r,有OC=R,O′O=h-R,则有(h-R)2+r2=R2,即r2=2Rh-h2.
∴V(h)=
| 1 |
| 3 |
| 2πRh2 |
| 3 |
| πh3 |
| 3 |
(2)V(h)=
| 1 |
| 6 |
| π |
| 6 |
| 4R-2h+h+h |
| 3 |
| 32 |
| 82 |
不等式取等号条件为4R-2h=h,即当h=
| 4 |
| 3 |
| 32 |
| 82 |
点评:本题考查函数模型的建立,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
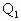 的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠
的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠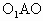 =θ.
=θ.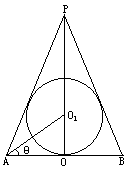
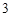 ,球内接圆锥的高为
,球内接圆锥的高为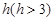 ,体积为
,体积为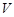 ,
,
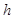 表示
表示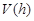 ;
;