题目内容
下列命题:①函数
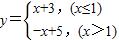 的最大值是4
的最大值是4②函数
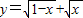 的定义域为{x|x≥1或x≤0}
的定义域为{x|x≥1或x≤0}③设a=0.7
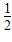 ,b=0.8
,b=0.8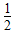 ,c=log30.7,则c<a<b
,c=log30.7,则c<a<b④集合A={x|0<log2x<1},B={x|x<a}若A⊆B,则a的范围是a≥2
其中正确的有 (请把所有满足题意的序号都填在横线上)
【答案】分析:①运用分段函数的单调性求解分段函数在整个定义域上的最大值;
②由两个根式有意义直接求出函数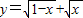 的定义域;
的定义域;
③运用幂函数的单调性和对数式的运算性质比较a、b、c的大小;
④根据子集的概念,借助于区间端点值的大小比较求得a的范围.
解答:解:①函数函数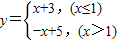 在x≤1时为增函数,在x>1时为减函数,
在x≤1时为增函数,在x>1时为减函数,
所以函数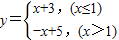 的最大值是4,所以①正确;
的最大值是4,所以①正确;
②由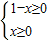 ⇒0≤x≤1,所以函数
⇒0≤x≤1,所以函数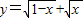 的定义域为{x|0≤x≤1},所以②不正确;
的定义域为{x|0≤x≤1},所以②不正确;
③因为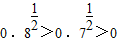 ,log30.7<0,所以c<a<b,所以③正确;
,log30.7<0,所以c<a<b,所以③正确;
④由A={x|0<log2x<1}={x|1<x<2},B={x|x<a},若A⊆B,则a的范围是a≥2,所以④正确.
所以正确的命题为①③④.
故答案为①③④.
点评:本题考查了命题真假的判断,考查了分段函数,分段函数的值域要分段求,最后取并集,集合之间的关系问题,重点在于区间端点值的大小比较.此题是基础题.
②由两个根式有意义直接求出函数
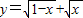 的定义域;
的定义域;③运用幂函数的单调性和对数式的运算性质比较a、b、c的大小;
④根据子集的概念,借助于区间端点值的大小比较求得a的范围.
解答:解:①函数函数
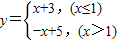 在x≤1时为增函数,在x>1时为减函数,
在x≤1时为增函数,在x>1时为减函数,所以函数
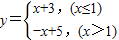 的最大值是4,所以①正确;
的最大值是4,所以①正确;②由
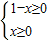 ⇒0≤x≤1,所以函数
⇒0≤x≤1,所以函数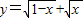 的定义域为{x|0≤x≤1},所以②不正确;
的定义域为{x|0≤x≤1},所以②不正确;③因为
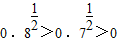 ,log30.7<0,所以c<a<b,所以③正确;
,log30.7<0,所以c<a<b,所以③正确;④由A={x|0<log2x<1}={x|1<x<2},B={x|x<a},若A⊆B,则a的范围是a≥2,所以④正确.
所以正确的命题为①③④.
故答案为①③④.
点评:本题考查了命题真假的判断,考查了分段函数,分段函数的值域要分段求,最后取并集,集合之间的关系问题,重点在于区间端点值的大小比较.此题是基础题.

练习册系列答案
相关题目
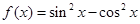 的最小正周期是
的最小正周期是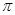 ;
;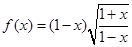 是偶函数;
是偶函数;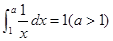 ,则
,则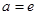 ;
;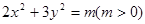 的离心率不确定。
的离心率不确定。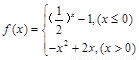 ,对于下列命题:
,对于下列命题: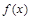 的最小值是0;
的最小值是0;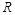 上是单调递减函数;
上是单调递减函数;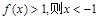 ;
;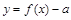 有三个零点,则
有三个零点,则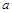 的取值范围是
的取值范围是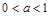 ;
;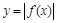 关于直线
关于直线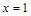 对称.
对称.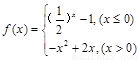 ,对于下列命题:
,对于下列命题: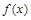 的最小值是0;
的最小值是0;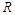 上是单调递减函数;
上是单调递减函数;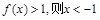 ;
;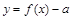 有三个零点,则
有三个零点,则 的取值范围是
的取值范围是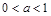 ;
;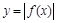 关于直线
关于直线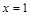 对称.
对称. 函数
函数 的最小正周期是
的最小正周期是 ;
;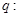 已知向量
已知向量 ,
, ,
, ,则
,则 的充要条件是
的充要条件是 ;
; 若
若 (
( ),则
),则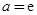 .其中所有的真命题是
.其中所有的真命题是 B.
B. C.
C. D.
D.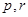
 函数
函数 的最小正周期是
的最小正周期是 ;
;
 ,使得
,使得 ;
; 已知向量
已知向量 ,
, ,
, ,则
,则 的充要条件是
的充要条件是 .
. B.
B. C.
C. D.
D.