题目内容
若3x=4y=36,则| 2 |
| x |
| 1 |
| y |
分析:由指数式和对数式的关系可得x=log336,y=log436,∴
+
=2×log363+log364,再利用对数的运算
性质化简求值.
| 2 |
| x |
| 1 |
| y |
性质化简求值.
解答:解:∵3x=4y=36,
∴x=log336,y=log436,
∴
+
=2×log363+log364=log369+log364=log3636=1,
故答案为 1.
∴x=log336,y=log436,
∴
| 2 |
| x |
| 1 |
| y |
故答案为 1.
点评:本题考查指数式和对数式的互化,对数的运算性质的应用,换底公式的应用.

练习册系列答案
相关题目
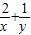 = .
= . = .
= .