题目内容
设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( )A.5
B.6
C.7
D.8
【答案】分析:根据二项式系数的性质求得a和b,再利用组合数的计算公式,解方程13a=7b求得m的值.
解答:解:∵m为正整数,由(x+y)2m展开式的二项式系数的最大值为a,以及二项式系数的性质可得a=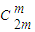 ,
,
同理,由(x+y)2m+1展开式的二项式系数的最大值为b,可得 b=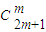 .
.
再由13a=7b,可得13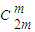 =7
=7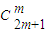 ,即 13×
,即 13×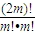 =7×
=7×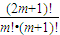 ,即 13=7×
,即 13=7×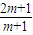 ,即 13(m+1)=7(2m+1).
,即 13(m+1)=7(2m+1).
解得m=6,
故选B.
点评:本题主要考查二项式系数的性质的应用,组合数的计算公式,属于中档题.
解答:解:∵m为正整数,由(x+y)2m展开式的二项式系数的最大值为a,以及二项式系数的性质可得a=
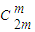 ,
,同理,由(x+y)2m+1展开式的二项式系数的最大值为b,可得 b=
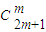 .
.再由13a=7b,可得13
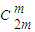 =7
=7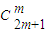 ,即 13×
,即 13×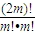 =7×
=7×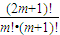 ,即 13=7×
,即 13=7×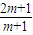 ,即 13(m+1)=7(2m+1).
,即 13(m+1)=7(2m+1).解得m=6,
故选B.
点评:本题主要考查二项式系数的性质的应用,组合数的计算公式,属于中档题.

练习册系列答案
相关题目