题目内容
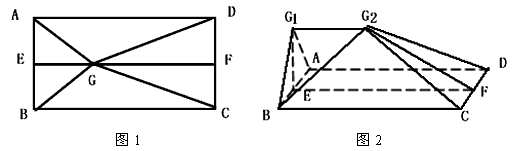
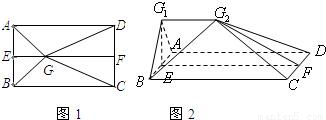
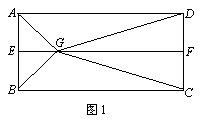
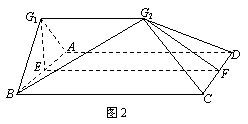
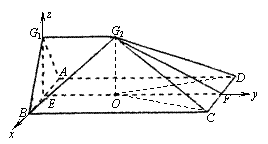
如图1,E、F分别是矩形ABCD的边AB、CD的中点,G是EF上的一点,将△GAB、△GCD分别沿AB、CD翻折成△G1AB、△G2CD,并连接G1G2,使平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD,连结BG2如图2.
(1) 证明平面G1AB⊥平面G1ADG2;
(2) 当AB = 12,BC = 25,EG = 8时,求直线BG2与平面G1ADG2成角.
 |
 |
||
解法一:
(1) ∵ 平面G1AB⊥平面ABCD,平面G1AB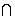 平面ABCD = AB,AD⊥AB,AD
平面ABCD = AB,AD⊥AB,AD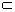 平面ABCD
平面ABCD
∴ AD⊥平面G1AB
又∵AD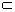 平面G1ADG2
平面G1ADG2
∴ 平面G1AB⊥平面G1ADG2 5分
(2) 过点B作BH⊥AG1于点H,连接G2H,由(1)的结论可知,BH⊥平面G1ADG2
∴ ∠BG2H是BG2和平面G1ADG2所成的角
∵ 平面G1AB⊥平面ABCD,平面G1AB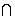 平面ABCD = AB,
平面ABCD = AB,
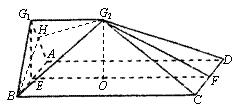
G1E⊥AB,G1E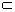 平面G1AB
平面G1AB
∴ G1E⊥平面ABCD,故G1E⊥EF
 ∵
G1G2 < AD,AD = EF
∵
G1G2 < AD,AD = EF
∴ 可在EF上取一点O,使EO = G1G2
又∵ G1G2∥AD∥EO
∴ 四边形G1EOG2是矩形
由题设AB = 12,BC = 25,EG = 8,则GF = 17
∴ G2O = G1E = 8,G2F =
17,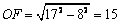 ,G1G2 = EO = 10
,G1G2 = EO = 10
∵ AD⊥平面G1AB,G1G2∥AD
∴ G1G2⊥平面G1AB,从而G1G2⊥G1B
故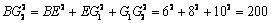 ,
,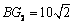
又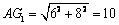 ,由
,由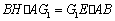 得
得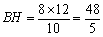
故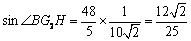
即直线BG2与平面G1ADG2所成的角是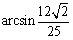 7分
7分
解法二:
(1) ∵ 平面G1AB⊥平面ABCD,平面G1AB 平面ABCD = AB,
平面ABCD = AB,
 G1E⊥AB,G1E
G1E⊥AB,G1E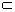 平面G1AB
平面G1AB
∴ G1E⊥平面ABCD,从而G1E⊥AD
又∵ AB⊥AD
∴ AD⊥平面G1AB
∵ AD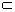 平面G1ADG2
平面G1ADG2
∴ 平面G1AB⊥平面G1ADG2 5分
(2) 由(1)可知,G1E⊥平面ABCD,故可以E为原点,分别以直线EB、EF、EG1为x轴、y轴、z轴建立空间直角坐标系,由题设AB = 12,BC = 25,EG = 8,则EB = 6,EF = 25,EG1 = 8,相关各点的坐标分别是A(–6,0,0),D(–6,25,0),G1(0,0,8),B(6,0,0),所以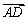 =(0,25,0),
=(0,25,0),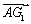 =(6,0,8)
=(6,0,8)
设n =(x,y,z)是平面G1ADG2的一个法向量
由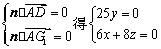 ,故可取n =(4,0,–3)
,故可取n =(4,0,–3)
过点G2作G2O⊥平面ABCD于点O,因为G2C = G2D,
∴ OC = OD,于是点O在y轴上
因为G1G2∥AD,所以G1G2∥EF,G2O = G1E = 8
设G2(0,m,8)(0 < m < 25),由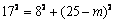 解得m = 10
解得m = 10
∴ 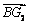 =(0,10,8)-(6,0,0)=(– 6,10,8)
=(0,10,8)-(6,0,0)=(– 6,10,8)
设BG2和平面G1ADG2所成的解是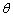 ,
,
则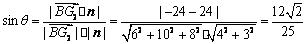
故直线BG2与平面G1ADG2所成的角是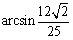 7分
7分

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案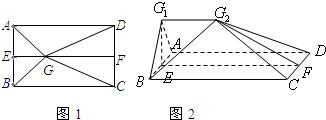 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2. 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.