题目内容
(江苏卷17)某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km, ![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
(I)按下列要求写出函数关系式:
设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;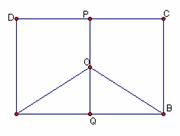
设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式。
的函数关系式。
(II)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短。
【解析】本小题主要考查函数最值的应用.
(Ⅰ)①由条件知PQ 垂直平分AB,若∠BAO=![]() (rad) ,则
(rad) ,则![]() , 故
, 故
![]() ,又OP=
,又OP=![]() ,
,
所以![]() ,
,
所求函数关系式为![]()
![]()
②若OP=![]() (km) ,则OQ=10-
(km) ,则OQ=10-![]() ,所以OA =OB=
,所以OA =OB=![]()
所求函数关系式为![]()
(Ⅱ)选择函数模型①,![]()
令![]() 0 得sin
0 得sin ![]() ,因为
,因为![]() ,所以
,所以![]() =
=![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是
是![]() 的减函数;当
的减函数;当![]() 时,
时,![]() ,
,![]() 是
是![]() 的增函数,所以当
的增函数,所以当![]() =
=![]() 时,
时,![]() 。这时点P 位于线段AB 的中垂线上,在矩形区域内且距离AB 边
。这时点P 位于线段AB 的中垂线上,在矩形区域内且距离AB 边![]() km处。
km处。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
