题目内容
ABCD为平行四边形,P为平面ABCD外一点,PA⊥面ABCD,且PA=AD=2,AB=1,AC=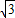 .
.(1)求证:平面ACD⊥平面PAC;
(2)求异面直线PC与BD所成角的余弦值;
(3)设二面角A-PC-B的大小为θ,试求tanθ的值.
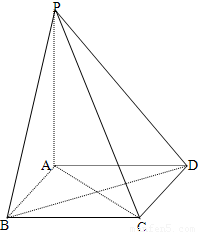
【答案】分析:(1)由已知中,PA⊥面ABCD,结合面面垂直的判定定理,我们易得平面ACD⊥平面PAC;
(2)令AC与BD交点为O,PA的中点为E,连接OE,则OE∥PC,则直线PC与BD所成角等于直线OE与BD所成角,解三角形OEB,即可得到答案.
(3)A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF,解三角形AEF,即可得到答案.
解答:证明:(1)∵PA⊥面ABCD,
PA?平面PAC
∴平面ACD⊥平面PAC;
解:(2)令AC与BD交点为O,PA的中点为E,连接OE,BE如图所示:
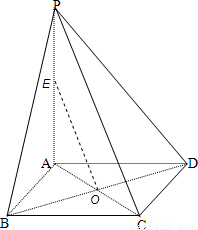
∵O为BD的中点,则EO= PC=
PC=
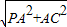 =
=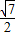 ,且OE∥PC
,且OE∥PC
又∵PA⊥面ABCD,且PA=AD=2,AB=1,AC=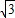 .
.
∴OB= BD=
BD=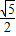 ,BE=
,BE=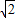
∴|cos∠EOB|=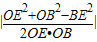 =
= ;
;
即异面直线PC与BD所成角的余弦值为 ;
;
(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF即∠AEF=θ.
在Rt△APC中,PC=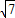 ,∴
,∴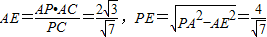 ,
,
在△PBC中,PB=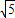 ,BC=2,∴
,BC=2,∴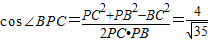 ,
,
在Rt△PEF中,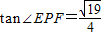 ,∴
,∴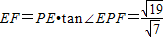
在△PAF中,PF=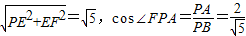 ,∴AF=1,
,∴AF=1,
在△AEF中,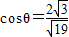 ,∴
,∴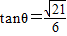
点评:本题考查的知识点是平面与平面垂直的判定,异面直线及其所成的角,二面角的平面角及求示,其中求二面角,关键是要找到二面角的平面角,将空间问题转化为一个平面解三角形的问题.
(2)令AC与BD交点为O,PA的中点为E,连接OE,则OE∥PC,则直线PC与BD所成角等于直线OE与BD所成角,解三角形OEB,即可得到答案.
(3)A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF,解三角形AEF,即可得到答案.
解答:证明:(1)∵PA⊥面ABCD,
PA?平面PAC
∴平面ACD⊥平面PAC;
解:(2)令AC与BD交点为O,PA的中点为E,连接OE,BE如图所示:

∵O为BD的中点,则EO=
 PC=
PC=
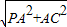 =
=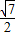 ,且OE∥PC
,且OE∥PC又∵PA⊥面ABCD,且PA=AD=2,AB=1,AC=
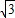 .
.∴OB=
 BD=
BD=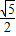 ,BE=
,BE=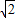
∴|cos∠EOB|=
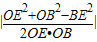 =
= ;
;即异面直线PC与BD所成角的余弦值为
 ;
;(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连接AE.则二面角A-PC-B的平面角为∠AEF即∠AEF=θ.
在Rt△APC中,PC=
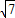 ,∴
,∴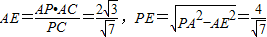 ,
,在△PBC中,PB=
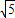 ,BC=2,∴
,BC=2,∴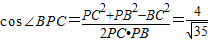 ,
,在Rt△PEF中,
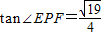 ,∴
,∴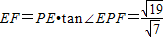
在△PAF中,PF=
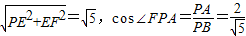 ,∴AF=1,
,∴AF=1,在△AEF中,
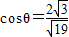 ,∴
,∴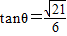
点评:本题考查的知识点是平面与平面垂直的判定,异面直线及其所成的角,二面角的平面角及求示,其中求二面角,关键是要找到二面角的平面角,将空间问题转化为一个平面解三角形的问题.

练习册系列答案
相关题目
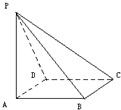 如图在四棱锥P-ABCD中,底面四边形ABCD为平行四边形,PA⊥面ABCD,PC•BD=0,PA=AB=2.∠BAD=60°.
如图在四棱锥P-ABCD中,底面四边形ABCD为平行四边形,PA⊥面ABCD,PC•BD=0,PA=AB=2.∠BAD=60°.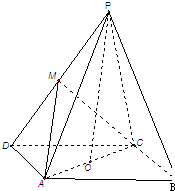 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.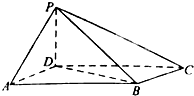 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. 如图,已知四棱锥P-ABCD.
如图,已知四棱锥P-ABCD.