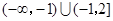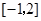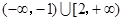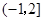题目内容
在数列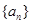 和
和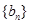 中,
中,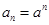 ,
,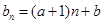 ,
,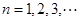 ,其中
,其中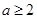 且
且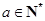 ,
,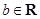 .设
.设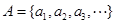 ,
,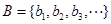 ,试问在区间
,试问在区间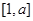 上是否存在实数
上是否存在实数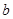 使得
使得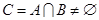 .若存在,求出
.若存在,求出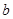 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合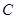 ;若不存在,试说明理由.
;若不存在,试说明理由.
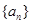 和
和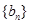 中,
中,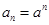 ,
,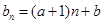 ,
,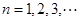 ,其中
,其中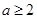 且
且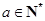 ,
,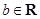 .设
.设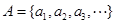 ,
,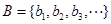 ,试问在区间
,试问在区间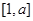 上是否存在实数
上是否存在实数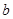 使得
使得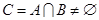 .若存在,求出
.若存在,求出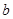 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合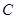 ;若不存在,试说明理由.
;若不存在,试说明理由.在区间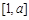 上存在实数
上存在实数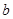 ,使
,使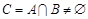 成立,当
成立,当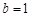 时,
时,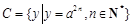 ;当
;当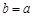 时,
时,
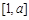 上存在实数
上存在实数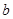 ,使
,使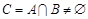 成立,当
成立,当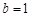 时,
时,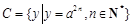 ;当
;当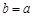 时,
时,
设存在实数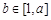 ,使
,使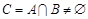 ,
,
设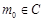 ,则
,则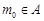 ,且
,且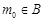 ,
,
设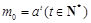 ,
, ,
,
则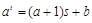 ,所以
,所以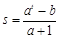 ,
,
因为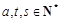 ,且
,且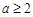 ,所以
,所以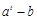 能被
能被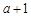 整除.
整除.
然后分三种情况讨论(1)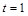 ;(2)
;(2) 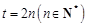 ;(3)
;(3) 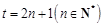 进行研究.
进行研究.
设存在实数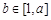 ,使
,使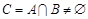 ,
,
设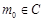 ,则
,则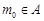 ,且
,且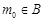 ,
,
设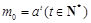 ,
, ,
,
则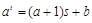 ,所以
,所以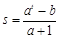 ,
,
因为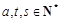 ,且
,且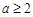 ,所以
,所以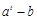 能被
能被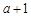 整除…………………………4分
整除…………………………4分
(1)当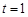 时,因为
时,因为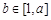 ,
, 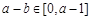 ,
,
所以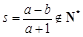 ; …………………………5分
; …………………………5分
(2)当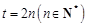 时,
时,
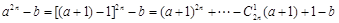 ,
,
由于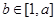 ,所以
,所以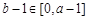 ,
,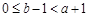 ,
,
所以,当且仅当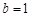 时,
时,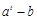 能被
能被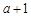 整除. …………………………7分
整除. …………………………7分
(3)当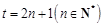 时,
时,
 ,
,
由于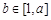 ,所以
,所以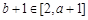 ,
,
所以,当且仅当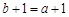 ,即
,即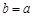 时,
时,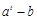 能被
能被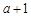 整除.………………9分
整除.………………9分
综上,在区间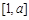 上存在实数
上存在实数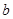 ,使
,使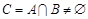 成立,
成立,
当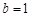 时,
时,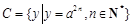 ;
;
当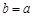 时,
时, .
.
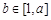 ,使
,使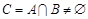 ,
,设
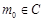 ,则
,则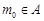 ,且
,且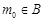 ,
,设
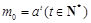 ,
, ,
,则
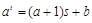 ,所以
,所以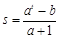 ,
,因为
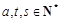 ,且
,且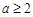 ,所以
,所以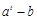 能被
能被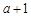 整除.
整除.然后分三种情况讨论(1)
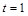 ;(2)
;(2) 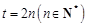 ;(3)
;(3) 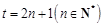 进行研究.
进行研究.设存在实数
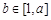 ,使
,使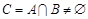 ,
,设
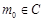 ,则
,则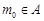 ,且
,且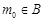 ,
,设
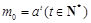 ,
, ,
,则
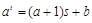 ,所以
,所以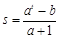 ,
,因为
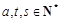 ,且
,且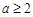 ,所以
,所以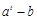 能被
能被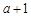 整除…………………………4分
整除…………………………4分(1)当
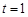 时,因为
时,因为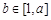 ,
, 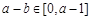 ,
,所以
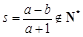 ; …………………………5分
; …………………………5分(2)当
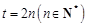 时,
时,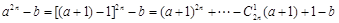 ,
,由于
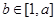 ,所以
,所以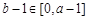 ,
,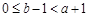 ,
,所以,当且仅当
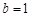 时,
时,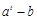 能被
能被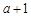 整除. …………………………7分
整除. …………………………7分(3)当
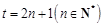 时,
时, ,
,由于
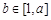 ,所以
,所以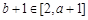 ,
,所以,当且仅当
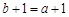 ,即
,即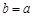 时,
时,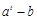 能被
能被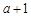 整除.………………9分
整除.………………9分综上,在区间
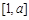 上存在实数
上存在实数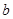 ,使
,使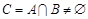 成立,
成立,当
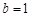 时,
时,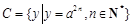 ;
;当
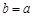 时,
时, .
.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
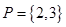 ,则
,则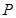 的所有子集的个数为___▲___.
的所有子集的个数为___▲___.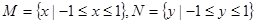 ,则在下列的图形中,不是从集合M到集合N的映射的是( ).
,则在下列的图形中,不是从集合M到集合N的映射的是( ).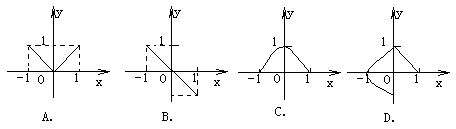
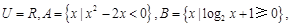 则
则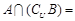 .
. 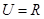 ,
,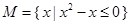 ,函数
,函数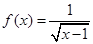 的定义域为
的定义域为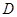 ,则
,则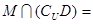 ( )
( )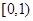
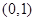
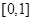
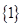
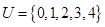 ,集合
,集合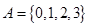 ,
,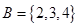 ,则
,则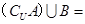 .
.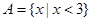 ,
,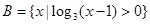 。则
。则 = .
= .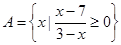 ,函数
,函数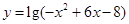 的定义域为集合
的定义域为集合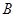 ,则
,则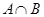 = .
= .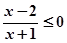 的解集是 ( )
的解集是 ( )