题目内容
与曲线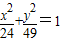 共焦点并且与曲线
共焦点并且与曲线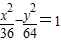 共渐近线的双曲线方程为 .
共渐近线的双曲线方程为 .
【答案】分析:先求出椭圆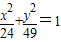 的焦点坐标,双曲线
的焦点坐标,双曲线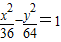 的渐近线方程,然后设双曲线的标准方程为
的渐近线方程,然后设双曲线的标准方程为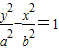 ,则根据此时双曲线的渐近线方程为y=±
,则根据此时双曲线的渐近线方程为y=±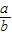 x,且有c2=a2+b2,可解得a、b,故双曲线方程得之.
x,且有c2=a2+b2,可解得a、b,故双曲线方程得之.
解答:解:由题意知椭圆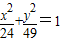 焦点在y轴上,且c=
焦点在y轴上,且c=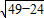 =5,
=5,
双曲线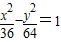 的渐近线方程为y=±
的渐近线方程为y=± x,
x,
设欲求双曲线方程为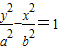 ,
,
则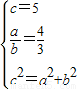 ,解得a=4,b=3,
,解得a=4,b=3,
所以欲求双曲线方程为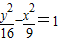 .
.
故答案为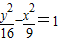 .
.
点评:本题主要考查焦点在不同坐标轴上的双曲线的标准方程与性质,同时考查椭圆的标准方程及简单性质.
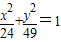 的焦点坐标,双曲线
的焦点坐标,双曲线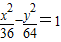 的渐近线方程,然后设双曲线的标准方程为
的渐近线方程,然后设双曲线的标准方程为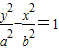 ,则根据此时双曲线的渐近线方程为y=±
,则根据此时双曲线的渐近线方程为y=±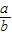 x,且有c2=a2+b2,可解得a、b,故双曲线方程得之.
x,且有c2=a2+b2,可解得a、b,故双曲线方程得之.解答:解:由题意知椭圆
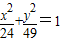 焦点在y轴上,且c=
焦点在y轴上,且c=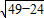 =5,
=5,双曲线
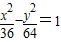 的渐近线方程为y=±
的渐近线方程为y=± x,
x,设欲求双曲线方程为
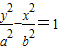 ,
,则
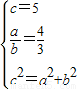 ,解得a=4,b=3,
,解得a=4,b=3,所以欲求双曲线方程为
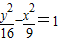 .
.故答案为
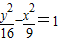 .
.点评:本题主要考查焦点在不同坐标轴上的双曲线的标准方程与性质,同时考查椭圆的标准方程及简单性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
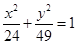 共焦点并且与曲线
共焦点并且与曲线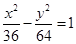 共渐近线的双曲线方程为 .
共渐近线的双曲线方程为 .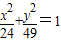 共焦点并且与曲线
共焦点并且与曲线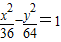 共渐近线的双曲线方程为 .
共渐近线的双曲线方程为 .