题目内容
A、B是直线y=1与函数 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .
.(1)求ω的值;
(2)在锐角△ABC中,a,b,c分别是角A,B,C的对边,若
 的面积为
的面积为 ,求a的值.
,求a的值.
【答案】分析:(1)化简函数f(x)的表达式,A、B是直线y=1与函数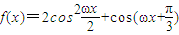 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .求出周期,然后求ω的值;
.求出周期,然后求ω的值;
(2) ,以及锐角△ABC求出A,由c=3,△ABC的面积为
,以及锐角△ABC求出A,由c=3,△ABC的面积为 ,求出b,利用余弦定理求a的值.
,求出b,利用余弦定理求a的值.
解答:解:(1)
由函数的图象及 ,得函数的周期
,得函数的周期 ,解得ω=2;
,解得ω=2;
(2)∵
∴
又∵△ABC是锐角三角形, ,
,
∴ ,即
,即
由 ,得b=4由余弦定理,
,得b=4由余弦定理,
得 ,即
,即
点评:本题考查三角函数的周期,余弦定理,三角形面积,是中档题.
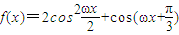 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .求出周期,然后求ω的值;
.求出周期,然后求ω的值;(2)
 ,以及锐角△ABC求出A,由c=3,△ABC的面积为
,以及锐角△ABC求出A,由c=3,△ABC的面积为 ,求出b,利用余弦定理求a的值.
,求出b,利用余弦定理求a的值.解答:解:(1)

由函数的图象及
 ,得函数的周期
,得函数的周期 ,解得ω=2;
,解得ω=2;(2)∵

∴

又∵△ABC是锐角三角形,
 ,
,∴
 ,即
,即
由
 ,得b=4由余弦定理,
,得b=4由余弦定理,得
 ,即
,即
点评:本题考查三角函数的周期,余弦定理,三角形面积,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且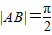 .
. 的面积为
的面积为 ,求a的值.
,求a的值.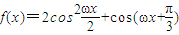 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .
. 的面积为
的面积为 ,求a的值.
,求a的值.