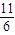题目内容
设a>1,函数y=|logax|的定义域为[m,n](m<n),值域为[0,1],定义“区间[m,n]的长度等于n-m”,若区间[m,n]长度的最小值为
,则实数a的值内( )
| 5 |
| 6 |
| A、11 | ||
| B、6 | ||
C、
| ||
D、
|
分析:本题考查的知识点是对数函数的性质,及函数图象的对折变换,为了方便分析,我们可以画出满足条件的图象,根据图象分析出正确的答案.
解答: 解:在坐标平面内先画出函数f(x)=logax的图象,
解:在坐标平面内先画出函数f(x)=logax的图象,
再将其图象位于x轴下方的部分“翻折”到x轴的上方,
与f(x)本身不在x轴下方的部分共同组成函数g(x)=|logax|的图象,
∵g(1)=0,g(a)=g(
)=1,
结合图形可知,要使函数g(x)的值域是[0,1],
其定义域可能是[
,1]、[1,a]、[
,a],
且1-
=
<a-1,
因此结合题意知1-
=
,
a=6.
故选B
 解:在坐标平面内先画出函数f(x)=logax的图象,
解:在坐标平面内先画出函数f(x)=logax的图象,再将其图象位于x轴下方的部分“翻折”到x轴的上方,
与f(x)本身不在x轴下方的部分共同组成函数g(x)=|logax|的图象,
∵g(1)=0,g(a)=g(
| 1 |
| a |
结合图形可知,要使函数g(x)的值域是[0,1],
其定义域可能是[
| 1 |
| a |
| 1 |
| a |
且1-
| 1 |
| a |
| a-1 |
| a |
因此结合题意知1-
| 1 |
| a |
| 5 |
| 6 |
a=6.
故选B
点评:中学数学研究的对象可分为数和形两大部分,数与形是有联系的,这个联系称之为数形结合,或形数结合.作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,或者借助形的几何直观性来阐明数之间某种关系,即数形结合包括两个方面:第一种情形是“以数解形”,而第二种情形是“以形助数”.“以数解形”就是有些图形太过于简单,直接观察却看不出什么规律来,这时就需要给图形赋值,如边长、角度等.

练习册系列答案
相关题目
设a>1,函数y=a|x|的图象形状大致是( )
A、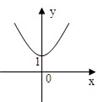 | B、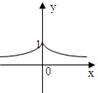 | C、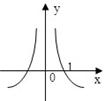 | D、 |
 ,则实数a的值内( )
,则实数a的值内( )