题目内容
已知f(x)= (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
 (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=
 的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。
的两个非零实根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由。解:(Ⅰ)f′(x)=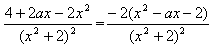 ,
,
∵f(x)在[-1,1]上是增函数,
∴f′(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立,①
设ψ(x)=x2-ax-2,
①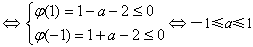 ,
,
∵对x∈[-1,1],f(x)是连续函数,
且只有当a=1时,f′(-1)=0以及当a=-1时,f′(1)=0,
∴A={a|-1≤a≤1};
(Ⅱ)由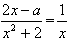 ,得x2-ax-2=0,
,得x2-ax-2=0,
∵△=a2+8>0,
∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,
从而|x1-x2|=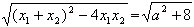 ,
,
∵-1≤a≤1,
∴|x1-x2|= ≤3,
≤3,
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立, ②
设g(t)=m2+tm-2=mt+(m2-2),
② g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0
g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0 m≥2或m≤-2,
m≥2或m≤-2,
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
其取值范围是{m|m≥2或m≤-2}。
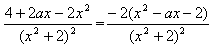 ,
,∵f(x)在[-1,1]上是增函数,
∴f′(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立,①
设ψ(x)=x2-ax-2,
①
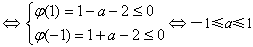 ,
,∵对x∈[-1,1],f(x)是连续函数,
且只有当a=1时,f′(-1)=0以及当a=-1时,f′(1)=0,
∴A={a|-1≤a≤1};
(Ⅱ)由
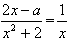 ,得x2-ax-2=0,
,得x2-ax-2=0, ∵△=a2+8>0,
∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,
从而|x1-x2|=
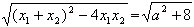 ,
,∵-1≤a≤1,
∴|x1-x2|=
 ≤3,
≤3,要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立, ②
设g(t)=m2+tm-2=mt+(m2-2),
②
 g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0
g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0 m≥2或m≤-2,
m≥2或m≤-2,所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
其取值范围是{m|m≥2或m≤-2}。

练习册系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则下列结论中正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、函数y=f(x)•g(x)的最大值为1 | ||||
B、函数y=f(x)•g(x)的对称中心是(
| ||||
C、当x∈[-
| ||||
D、将f(x)的图象向右平移
|
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.