题目内容

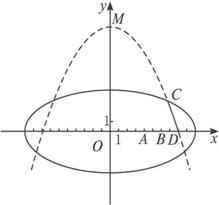
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图.航天器运行(按顺时针方向)的轨迹方程为+=1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.

(1)求航天器变轨后的运行轨迹所在的曲线方程;

(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?

解：(1)设曲线方程为y=ax2+,由题意可知0=a·64+.

∴a=-.

∴曲线方程为y=-x2+.

(2)设变轨点为C(x,y),根据题意可知

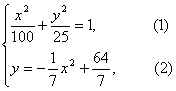
整理,得4y2-7y-36=0,

y=4或y=-(不合题意,舍去).

由y=4

得x=6或x=-6(不合题意,舍去).

∴C点的坐标为(6,4),|AC|=2,|BC|=4.

答:当观测点A、B测得AC、BC的距离分别为2和4时,应向航天器发出变轨指令.


练习册系列答案
相关题目
精英家教网学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如图：航天器运行（按顺时针方向）的轨迹方程为
x2
100
+
y2
25
=1，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y轴为对称轴、M(0，
64
7
)为顶点的抛物线的实线部分，降落点为D（8，0）．观测点A（4，0）、B（6，0）同时跟踪航天器．
（1）求航天器变轨后的运行轨迹所在的曲线方程；
（2）试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时，应向航天器发出变轨指令？
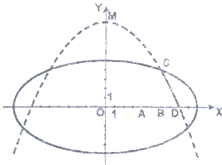（2006•蚌埠二模）“神六”上天并顺利返回，让越来越多的青少年对航天技术发生了兴趣．某学校科技小组在计算机上模拟航天器变轨返回试验，设计方案
如图：航天器运行（按顺时针方向）的轨迹方程为
x2
100
+
y2
25
=1，变轨（航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y轴为
对称轴、M（0，
64
7
）为顶点的抛物线的实线部分，降落点为D（8，0），观测点A（4，0）、B（6，0）同时跟踪航天器．试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为
2
5
、4
2
5
、4
时航天器发出变轨指令．
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如下图：航天器运行(按顺时针方向)的轨迹方程为=1，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,)为顶点的抛物线的实线部分，降落点为D(8,0).观测点A(4,0)、B(6，0)同时跟踪航天器.

(1)求航天器变轨后的运行轨迹所在的曲线方程；

(2)试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时.应向航天器发出变轨指令？

学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图：航天器运行（按顺时针方向）的轨迹方程为，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以轴为对称轴、 为顶点的抛物线的实线部分，降落点为. 观测点同时跟踪航天器.求航天器变轨后的运行轨迹所在的曲线方程。

学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图：航天器运行（按顺时针方向）的轨迹方程为，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以轴为对称轴、 为顶点的抛物线的实线部分，降落点为. 观测点同时跟踪航天器. 试问：当航天器在轴上方时，观测点测得离航天器的距离分别为多少时，应向航天器发出变轨指令？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网