题目内容
某农贸公司按每担200元收购某农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购a万担．政府为了鼓励收购公司多收购这种农产品，决定征税率降低x（x≠0）个百分点，预测收购量可增加2x个百分点．（Ⅰ）写出税收y（万元）与x的函数关系式；
（Ⅱ）要使此项税收在税率调节后，不少于原计划税收的83.2%，试确定x的取值范围．
【答案】分析：（Ⅰ）根据征税率降低x（x≠0）个百分点，预测收购量可增加2x个百分点，可知降低税率后的税率为（10-x）%，农产品的收购量为a（1+2x%）万担，收购总金额 200a（1+2x%），从而可求税收y（万元）与x的函数关系式；
（Ⅱ）利用税收在税率调节后，不少于原计划税收的83.2%，可建立不等关系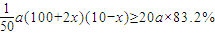
，从而可得x的取值范围．
解答：解：（Ⅰ）降低税率后的税率为（10-x）%，农产品的收购量为a（1+2x%）万担，收购总金额 200a（1+2x%），…（6分）
依题意：
．…（2分）
（Ⅱ）原计划税收为200a•10%=20a（万元）．
依题意得：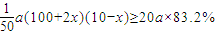
，…（6分）
化简得，x2+40x-84≤0，，∴-42≤x≤2．又∵0＜x＜10，∴0＜x≤2．
答：x的取值范围是0＜x≤2．…（2分）
点评：本题的考点是根据实际问题选择函数类型，主要考查二次函数模型，关键是从实际问题中抽象出函数模型，考查学生的分析解决问题的能力．
（Ⅱ）利用税收在税率调节后，不少于原计划税收的83.2%，可建立不等关系
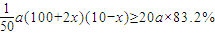，从而可得x的取值范围．解答：解：（Ⅰ）降低税率后的税率为（10-x）%，农产品的收购量为a（1+2x%）万担，收购总金额 200a（1+2x%），…（6分）
依题意：
．…（2分）（Ⅱ）原计划税收为200a•10%=20a（万元）．
依题意得：
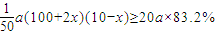，…（6分）化简得，x2+40x-84≤0，，∴-42≤x≤2．又∵0＜x＜10，∴0＜x≤2．
答：x的取值范围是0＜x≤2．…（2分）
点评：本题的考点是根据实际问题选择函数类型，主要考查二次函数模型，关键是从实际问题中抽象出函数模型，考查学生的分析解决问题的能力．
练习册系列答案
相关题目