题目内容
设a>0，
是R上的偶函数。
（1）求a的值。
（2）证明：f(x)在(0，+¥)上是增函数。
答案：
解析：
解析：
解（1）因为函数 是R上的偶函数，所以f(-x)=f(x)
即 因此 （2）由 当xÎ(0，+¥)时，由指数函数的性质知e-x>0，e2x>1，∴ f ¢(x)>0，因此函数
|
故
由于ex-e-x¹0
，又a>0，所以a=1。
，∴f ¢(x)=ex-e-x=e-x(e2x-1)
在(0，+¥)上是增函数。
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
是
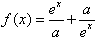是R上的偶函数。
是R上的偶函数。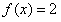
。