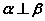题目内容
设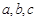 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不正确的是( )
是空间两个平面,则下列命题中,逆命题不正确的是( )
A.当 时,若
时,若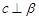 ,则
,则
B.当 时,若
时,若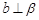 ,则
,则
C.当 且
且 是
是 在
在 内的射影时,若
内的射影时,若 ,则
,则
D.当 且
且 时,若
时,若 ,则
,则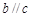
【答案】
B
【解析】
试题分析:分别写出其逆命题再判断,A、由面面平行的性质定理判断.B、也可能平行C、由三垂线定理判断.D、由线面平行的判定定理判断.
A、其逆命题是:当c⊥α时,或α∥β,则c⊥β,由面面平行的性质定理知正确.
B、其逆命题是:当b⊂α,若α⊥β,则b⊥β,也可能平行,相交.不正确.
C、其逆命题是当b⊂α,且c是a在α内的射影时,若a⊥b,则b⊥c,由三垂线定理知正确.
D、其逆命题是当b⊂α,且c⊄α时,若b∥c,则c∥α,由线面平行的判定定理知正确.
故选B
考点:本题主要考查线面平行的判定理,三垂线定理及其逆定理,面面平行的性质定理等,做这样的题目要多观察几何体效果会更好.
点评:解决该试题的关键是熟练运用线面平行的判定定理和性质定理,和线面垂直的判定定理和性质定理的运用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当 时,若 时,若 ,则 ,则 |
B.当 ,且 ,且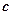 是 是 在 在 内的射影时,若 内的射影时,若 ,则 ,则 |
C.当 ,且 ,且 时,若 时,若 ,则 ,则 |
D.当 时,若 时,若 ,则 ,则 |
 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( ) 时,若
时,若 ,则
,则
 ,且
,且 是
是 在
在 内的射影时,若
内的射影时,若 ,则
,则
 时,若
时,若 ,则
,则
 ,则
,则
 是空间三条直线,
是空间三条直线, 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( ) 时,若
时,若 ,则
,则
 ,且
,且 是
是 在
在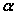 内的射影时,若
内的射影时,若 ,则
,则
 时,若
时,若 ,则
,则
 ,则
,则