题目内容
若函数 的零点个数为
的零点个数为 ,则
,则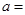 __ __ _
__ __ _
4
解析试题分析:令函数f(x)=|x2-4x|-a=0,可得|x2-4x|=a.
由于函数f(x)=|x2-4x|-a的零点个数为3,故函数y=|x2-4x|的图象和函数y=a的图象有3个交点,
如图所示: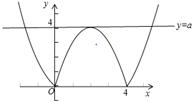
故a=4.
故答案为 4.
考点:本题主要是考查函数的零点与方程的根的关系,体现了化归与转化的数学思想,属于中档题.
点评:解决该试题的关键是由题意可得函数y=|4x-x2|与函数y=a有3个交点,结合图象可得实数a的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 和
和 ,定义运算“﹡”:
,定义运算“﹡”:
 ,设
,设 ,且关于
,且关于 的方程
的方程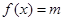 恰有一个实数根,则实数
恰有一个实数根,则实数 的取值范围是______________.
的取值范围是______________. 和双曲余弦函数
和双曲余弦函数 ,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。 ,则
,则 。
。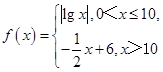 若
若 互不相等,且
互不相等,且 ,则
,则 的取值范围是 .
的取值范围是 .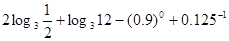 =_____________
=_____________ ,则满足不等式
,则满足不等式 >
> 的x的取值范围是___________________。
的x的取值范围是___________________。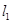 ::y="m" 和
::y="m" 和 :y=
:y= (m>0),直线
(m>0),直线 的图像从左至右相交于点A,B , 直线
的图像从左至右相交于点A,B , 直线 的最小值为 .
的最小值为 .