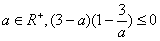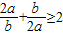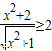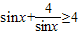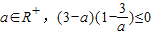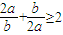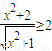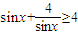题目内容
下列结论中,错用基本不等式做依据的是( )
A、a,b均为负数,则
| ||||
B、
| ||||
C、sinx+
| ||||
D、a∈R+,(3-a)(1-
|
分析:使用均值不等式解题必须满足三个基本条件:“一正,二定、三相等”.根据均值不等式解题必须满足三个基本条件:“一正,二定、三相等”可知A、B、D均满足条件.C选项中sinx≠±2,不满足“相等”的条件,再者sinx可以取到负值.
解答:解:根据均值不等式解题必须满足三个基本条件:“一正,二定、三相等”可知A、B、D均满足条件.
对于C选项中sinx≠±2,
不满足“相等”的条件,
再者sinx可以取到负值.
故选C.
对于C选项中sinx≠±2,
不满足“相等”的条件,
再者sinx可以取到负值.
故选C.
点评:本题考查基本不等式的应用,解题时要灵活运用公式进行解题.

练习册系列答案
相关题目
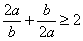 B.
B.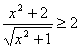
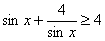 D.
D.