题目内容
已知函数 .
.
(1)当 时,求函数
时,求函数 的定义域;
的定义域;
(2)若关于 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求函数
时,求函数 的定义域;
的定义域;(2)若关于
 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.(1)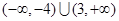 ;(2)
;(2)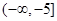 .
.
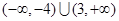 ;(2)
;(2)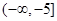 .
.试题分析:本题考查绝对值不等式的解法和不等式的恒成立问题,考查学生的分类讨论思想和转化能力.第一问,先将
 代入,定义域只需真数大于0,所以解绝对值不等式,利用函数的零点分段讨论解不等式组;第二问,将问题转化为恒成立问题,转化为求函数最值问题,利用
代入,定义域只需真数大于0,所以解绝对值不等式,利用函数的零点分段讨论解不等式组;第二问,将问题转化为恒成立问题,转化为求函数最值问题,利用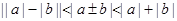 求函数
求函数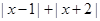 的最小值.
的最小值.试题解析:(1)由题设知:
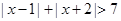 ,
,不等式的解集是以下不等式组解集的并集:
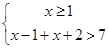 或
或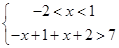 或
或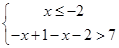 3分
3分解得函数
 的定义域为
的定义域为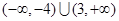 . 5分
. 5分(2)不等式
 即
即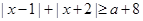 ,
,∵
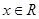 ,恒有,
,恒有,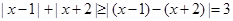 , 7分
, 7分∵不等式
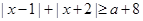 解集是
解集是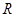 ,
,∴
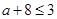
∴
 的取值范围是
的取值范围是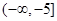 . 10分
. 10分
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目





 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围. 及其反函数的图象与函数
及其反函数的图象与函数 的图象交于A、B两点,若
的图象交于A、B两点,若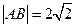 ,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 )
,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827 lg 8.392 ≈ 0.9293 lg 8.41 ≈ 0.9247 ) .
. 和
和 (其中
(其中 ),
), 与函数
与函数 的图像从左至右相交于点
的图像从左至右相交于点 ,
, ,
, 与函数
与函数 ,
, .记线段
.记线段 和
和 在
在 轴上的投影长度分别为
轴上的投影长度分别为 .当
.当 变化时,
变化时, 的最小值为( )
的最小值为( )



 ,
, ,求
,求 的范围; (2)不等式
的范围; (2)不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 .
.  ;
;  ,求证:
,求证: ≤
≤ .
. ,
, ,函数
,函数 ,
, 且
且 ,则
,则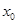 的取值范围是 .
的取值范围是 .