题目内容
选做题(从下列二题中任选做一题,若两题全做,则只按一题计分)
(优选法和实验设计初步选做题)某化工厂准备对一化工产品进行技术改造,决定优选加工温度,假定最佳温度在60°C到81°C之间,现用分数发进行优选,则第二个试点的温度为
(坐标系与参数方程选做题)在极坐标系中,定点A(1,
),动点B在曲线ρ=2cosθ上移动,当线段AB最短时,点B的极径为
.
(优选法和实验设计初步选做题)某化工厂准备对一化工产品进行技术改造,决定优选加工温度,假定最佳温度在60°C到81°C之间,现用分数发进行优选,则第二个试点的温度为
68°C
68°C
.(坐标系与参数方程选做题)在极坐标系中,定点A(1,
| π |
| 2 |
2-
|
2-
|
分析:由题知试验范围为[60,81],区间长度为21,故可把该区间等分成21段,利用分数法选取试点进行计算;
在极坐标系中,线段AB最短,B就是过A与圆心的直线和圆的交点,利用余弦定理即可求得点B的极径OB的长即可.
在极坐标系中,线段AB最短,B就是过A与圆心的直线和圆的交点,利用余弦定理即可求得点B的极径OB的长即可.
解答:解:由已知试验范围为[60,81],可得区间长度为21,将其等分21段,
利用分数法选取试点:x1=60+
×(81-20)=73,x2=60+81-73=68,
由对称性可知,第二次试点是68°C.
在极坐标系中,定点A(1,
),曲线ρ=2cosθ表示圆心在Q(1,0),半径为1的圆,如图.
线段AB最短,B就是过A与圆心的直线和圆的交点,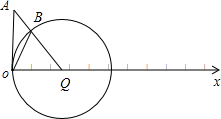
在△OBQ中,由余弦定理得:
OB2=OQ2+QB2-2OQ•QBcos∠OQB=
,
所以点B的极径为
故答案为:68°C;
利用分数法选取试点:x1=60+
| 13 |
| 21 |
由对称性可知,第二次试点是68°C.
在极坐标系中,定点A(1,
| π |
| 2 |
线段AB最短,B就是过A与圆心的直线和圆的交点,

在△OBQ中,由余弦定理得:
OB2=OQ2+QB2-2OQ•QBcos∠OQB=
2-
|
所以点B的极径为
2-
|
故答案为:68°C;
2-
|
点评:本题考查的是分数法的简单应用,考查极坐标与直角坐标的互化,掌握极坐标与一般方程之间的转化是关键.

练习册系列答案
相关题目