题目内容
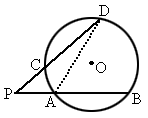
同学们知道:顶点在圆上,并且两边都和圆相交的角叫圆周角.因为一条弧所对的圆周角等于它所对的圆心角的一半,而圆心角的度数等于它所对弧的度数,所以圆周角的度数等于它所对弧的度数的一半.类似地,我们定义:顶点在圆外,并且两边和圆相交的角叫圆外角.如下图,∠
DPB是圆外角,那么∠DPB的度数与它所夹的两段弧 和
和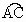 的度数有什么关系?
的度数有什么关系?
答案:略
解析:
提示:
解析:
|
解:连结 AD,由三角形外角等于与它不相邻的两内角的和,可得∠DAB=∠DPB+∠D,因此∠DPB=∠DAB-∠D.而∠ DAB、∠D的度数分别是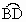 和 和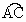 度数的一半. 度数的一半.
所以∠ DPB的度数是它所夹两段弧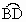 和 和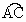 度数的差的一半. 度数的差的一半. |
提示:
|
分析:要想知道∠DPB与两段弧 |

练习册系列答案
相关题目