��Ŀ����
һ�������������������أ�2011��1�¾����������Σ������У��ó���һ���µ���Ⱦ��Ϊ60�����κ�ǰ�ĸ��µ���Ⱦ�����±���| ���� | 1 | 2 | 3 | 4 | �� |
| ��Ⱦ�� | 60 | 31 | 13 | �� |
 ��h��x��=30|log2x-2|��x��1��������x��ʾ������f��x����g��x����h��x���ֱ��ʾ��Ⱦ�ȣ����ο����ݣ�lg2=0.3010��lg3=0.4771��
��h��x��=30|log2x-2|��x��1��������x��ʾ������f��x����g��x����h��x���ֱ��ʾ��Ⱦ�ȣ����ο����ݣ�lg2=0.3010��lg3=0.4771��������ѡ���ĸ�����ģ��ȽϺ�������˵�����ɣ�
���������������Ҫ��ó�ÿ�µ����۶Ⱦ����ܳ���60�����ԱȽϺ�����ģ�⺯��Ԥ�⣬�ó������ں�ʱ��ʼ�����ٴ����Σ�
���𰸡���������1��ͨ������f��1����f��2����f��3����g��1����g��2����g��3����h��1����h��2����h��3����ֵ����֪h��x�����ӽ����е�ʵ��ֵ����h��x��ģ���Ϊ������
��2���ɸ��Ϻ����ĵ�����֪��ȷ������h��x����x��4��������������h��16��=60���ʿɵý��ۣ�
����⣺����������֪f��2��=40��g��2����26.7��h��2��=30 ����3�֣�
f��3��=20��g��3����6.7��h��3����12.5 ����6�֣�
�ɴ˿ɵ�h��x�����ӽ�ʵ��ֵ��������h��x��ģ��ȽϺ���������7�֣�
������h��x��=30|log2x-2|��x��4����������������Ϊh��16��=60 ����12�֣�
��˵����һ�����κ���16���µ���Ⱦ�Ȳ�����60��
��Ӧ��2012��5����ʼ�ٴ����Σ�����14�֣�
���������⿼���˺���ģ�͵�ѡ����Ӧ�����⣬ѡ����ģ��ʵ������ʱ������ֵԽ�ӽ�ʵ��ֵ������ģ��Ч��Խ�ã�
��2���ɸ��Ϻ����ĵ�����֪��ȷ������h��x����x��4��������������h��16��=60���ʿɵý��ۣ�
����⣺����������֪f��2��=40��g��2����26.7��h��2��=30 ����3�֣�
f��3��=20��g��3����6.7��h��3����12.5 ����6�֣�
�ɴ˿ɵ�h��x�����ӽ�ʵ��ֵ��������h��x��ģ��ȽϺ���������7�֣�
������h��x��=30|log2x-2|��x��4����������������Ϊh��16��=60 ����12�֣�
��˵����һ�����κ���16���µ���Ⱦ�Ȳ�����60��
��Ӧ��2012��5����ʼ�ٴ����Σ�����14�֣�
���������⿼���˺���ģ�͵�ѡ����Ӧ�����⣬ѡ����ģ��ʵ������ʱ������ֵԽ�ӽ�ʵ��ֵ������ģ��Ч��Խ�ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
һ�������������������أ�2011��1�¾����������Σ������У��ó���һ���µ���Ⱦ��Ϊ60�����κ�ǰ�ĸ��µ���Ⱦ�����±���
| ���� | 1 | 2 | 3 | 4 | �� |
| ��Ⱦ�� | 60 | 31 | 13 | 0 | �� |
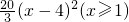 ��h��x��=30|log2x-2|��x��1��������x��ʾ������f��x����g��x����h��x���ֱ��ʾ��Ⱦ�ȣ����ο����ݣ�lg2=0.3010��lg3=0.4771��
��h��x��=30|log2x-2|��x��1��������x��ʾ������f��x����g��x����h��x���ֱ��ʾ��Ⱦ�ȣ����ο����ݣ�lg2=0.3010��lg3=0.4771��������ѡ���ĸ�����ģ��ȽϺ�������˵�����ɣ�
���������������Ҫ��ó�ÿ�µ����۶Ⱦ����ܳ���60�����ԱȽϺ�����ģ�⺯��Ԥ�⣬�ó������ں�ʱ��ʼ�����ٴ����Σ�

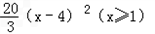 ��
��