题目内容
设关于x的不等式组
|
分析:由条件|x+1|<2得-3<x<1.A∩Z共有两个元素,说明不等式x2+2ax+3<0的解的集合的区间长度有着限制.
解答:解:由条件|x+1|<2得-3<x<1.由分析知,不等式x2+2ax+3-a<0的解的集合的区间长度有着限制,
也即方程x2+2ax+3-a=0的解的集合的区间长度有着限制,设f(x)=x2+2ax+3-a
则有f(0.5)=3.25>0,结合-3<x<1和抛物线的图象,
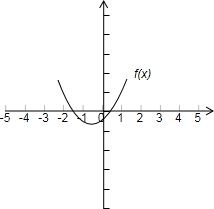
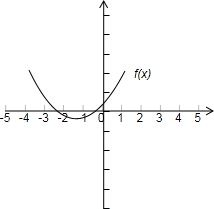
得
或
解之得,实数a的取值范围为(
,3]
故填(
,3].
也即方程x2+2ax+3-a=0的解的集合的区间长度有着限制,设f(x)=x2+2ax+3-a
则有f(0.5)=3.25>0,结合-3<x<1和抛物线的图象,


得
|
|
解之得,实数a的取值范围为(
| 7 |
| 5 |
故填(
| 7 |
| 5 |
点评:本题属于难题了,难在对于条件的转化,难在数形结合思想的应用.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 解集为A,Z为整数集,且A∩Z共有两个元素,则实数a的取值范围为________.
解集为A,Z为整数集,且A∩Z共有两个元素,则实数a的取值范围为________. 解集为A,Z为整数集,且A∩Z共有两个元素,则实数a的取值范围为 .
解集为A,Z为整数集,且A∩Z共有两个元素,则实数a的取值范围为 .