题目内容
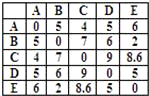 某旅游城市有5个景点,这5个景点间的路线距离(单位:十公里)见右表,若以景点A为起点,景点E为终点,每个景点经过且只经过一次,那么旅游公司开发的最短路线距离为
某旅游城市有5个景点,这5个景点间的路线距离(单位:十公里)见右表,若以景点A为起点,景点E为终点,每个景点经过且只经过一次,那么旅游公司开发的最短路线距离为
- A.20.6
- B.21
- C.22
- D.23
B
分析:本题考查的是函数的最值应用问题.在解答时可以根据列表逐一列举出所有可能的路线,然后计算出相应的距离,进而比较数据即可获得问题的解答.
解答:由题意可知:以景点A为起点,景点E为终点,旅游公司可开发的路线有
A-B-C-D-E、A-B-D-C-E、A-C-B-D-E、A-C-D-B-E、A-D-B-C-E、A-D-C-B-E,
其路线距离分别为:26、28.6、22、21、26.6、23,
故旅游公司开发的最短路线距离为21.
故选B.
点评:本题考查的是函数的最值应用问题.在解答的过程当中充分体现了实际背景的利用、列举的思想、读图和计算的能力.值得同学们体会反思.
分析:本题考查的是函数的最值应用问题.在解答时可以根据列表逐一列举出所有可能的路线,然后计算出相应的距离,进而比较数据即可获得问题的解答.
解答:由题意可知:以景点A为起点,景点E为终点,旅游公司可开发的路线有
A-B-C-D-E、A-B-D-C-E、A-C-B-D-E、A-C-D-B-E、A-D-B-C-E、A-D-C-B-E,
其路线距离分别为:26、28.6、22、21、26.6、23,
故旅游公司开发的最短路线距离为21.
故选B.
点评:本题考查的是函数的最值应用问题.在解答的过程当中充分体现了实际背景的利用、列举的思想、读图和计算的能力.值得同学们体会反思.

练习册系列答案
相关题目
 11、某旅游城市有5个景点,这5个景点间的路线距离(单位:十公里)见右表,若以景点A为起点,景点E为终点,每个景点经过且只经过一次,那么旅游公司开发的最短路线距离为( )
11、某旅游城市有5个景点,这5个景点间的路线距离(单位:十公里)见右表,若以景点A为起点,景点E为终点,每个景点经过且只经过一次,那么旅游公司开发的最短路线距离为( )

