题目内容
已知等差数列{an}满足a2=3,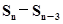 =51(n>3) ,
=51(n>3) ,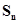 = 100,则n的值为
= 100,则n的值为
| A.8 | B.9 | C.10 | D.11 |
C
解析试题分析:由已知得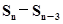 =51,即
=51,即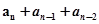 =51,而
=51,而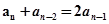 ,所以
,所以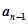 =17,
=17,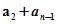 =
= 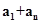 ,故由
,故由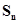 =
=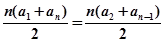 =100,得n=10,故选C。
=100,得n=10,故选C。
考点:本题主要考查等差数列的通项公式,求和公式,等差数列的性质。
点评:基础题,本题综合考查等差数列的基础知识,本解答主要利用等差数列的性质m+n="p+q," 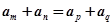 ,运用方程思想,求得n。
,运用方程思想,求得n。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知数列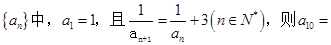
| A.28 | B.33 | C.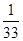 | D.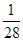 |
设Sn是等差数列{an}的前n项和,若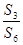 =
=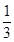 ,则
,则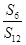 = ( )
= ( )
A.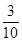 | B.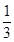 | C. | D. |
等差数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列。
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 2 | 3 | 5 |
| 第二行 | 8 | 6 | 14 |
| 第三行 | 11 | 9 | 13 |
则a4的值为
A.18 B.15 C.12 D.20
首项为 的等差数列,从第10项起开始为正数,则公差d的取值范围是
的等差数列,从第10项起开始为正数,则公差d的取值范围是
A.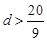 | B.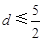 | C.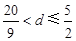 | D.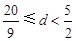 |
数列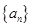 的首项为
的首项为 ,
,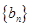 为等差数列且
为等差数列且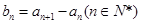 .若则
.若则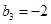 ,
,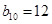 ,则
,则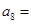 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
设Sn是等差数列{an}的前n项和,a12=-8,S9=-9,则S16= ( )
| A.-72 | B.72 | C.36 | D.-36 |
等差数列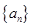 的前n项和为
的前n项和为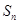 ,已知
,已知 ,
,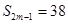 ,则
,则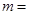 ( )
( )
| A.38 | B.20 | C.10 | D.9 |
等差数列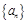 中,若
中,若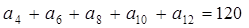 ,则
,则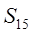 的值为:
的值为:
| A.180 | B.240 | C.360 | D.720 |