题目内容
已知：A（0，8），B（-4，0），C（m，-4），三点共线，则实数m的值是
- A.-6
- B.-2
- C.2
- D.6
A
分析：三点共线时，三个点构成的某两个向量互相平行，用向量平行的坐标条件即可解题．直线斜率存在时，用直线的斜率相等也可解题
解答：
方法一：∵A、B、C三点共线
∴
∥
又∵A（0，8），B（-4，0），C（m，-4）
∴
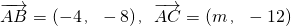
∴48+8m=0
∴m=-6
方法二：由题意知，直线的斜率存在
∴KAB=KAC
即：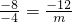
∴m=-6
故选A
点评：本题考查点共线问题，向量平行的坐标条件，直线斜率的表示．属简单题
分析：三点共线时，三个点构成的某两个向量互相平行，用向量平行的坐标条件即可解题．直线斜率存在时，用直线的斜率相等也可解题
解答：
方法一：∵A、B、C三点共线
∴
∥又∵A（0，8），B（-4，0），C（m，-4）
∴
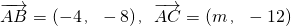
∴48+8m=0
∴m=-6
方法二：由题意知，直线的斜率存在
∴KAB=KAC
即：
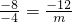
∴m=-6
故选A
点评：本题考查点共线问题，向量平行的坐标条件，直线斜率的表示．属简单题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
=（-2，4）平移到F'，已知点A（0，8）在F'上，F与F'的交点是B
，试求F对应的函数解析式．