题目内容
下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)也是增函数,则函数f(x)在R上是增函数;
②若f(2)=f(-2),则函数f(x)不是奇函数;
③函数f(x)=-
的单调增区间是(-∞,0)∪(0,+∞)
④对应法则和值域相同的函数的定义域也相同;
⑤函数的定义域一定不是空集;
写出上述所有正确结论的序号:______.
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)也是增函数,则函数f(x)在R上是增函数;
②若f(2)=f(-2),则函数f(x)不是奇函数;
③函数f(x)=-
| 1 |
| x |
④对应法则和值域相同的函数的定义域也相同;
⑤函数的定义域一定不是空集;
写出上述所有正确结论的序号:______.
①由增函数的定义中“任意性”知,两个单调区间不能并在一起,故不对;
②函数y=0(x∈R)既是奇函数又是偶函数,但f(2)=f(-2),故不对;
③考察幂函数函数f(x)=-
| 1 |
| x |
④考察函数y=0(x∈R),但当定义域不同时,函数对应法则和值域可以相同,故不对;
⑤根据函数的定义知函数的定义域一定不是空集,⑤正确..
故答案为⑤

练习册系列答案
相关题目
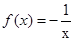 的单调增区间是(-∞,0)
的单调增区间是(-∞,0) (0,+∞)
(0,+∞)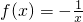 的单调增区间是(-∞,0)∪(0,+∞)
的单调增区间是(-∞,0)∪(0,+∞)