题目内容
在半径为R的球面上有不同的三点A、B、C，已知A、B、C三点中任意两点的球面距离均为| π | 3 |
分析：任意两点的球面距离均为
R．推出∠AOC=∠AOB=∠BOC=60°，推出三棱锥为正四面体，然后求正四面体体积．
| π |
| 3 |
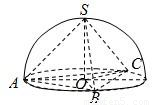
解答：
解：由题意可知三棱锥是正四面体，棱长为R，如图，
所以正四面体的体积：
×
R2×
=
R3，
故答案为：
R3．
解：由题意可知三棱锥是正四面体，棱长为R，如图，所以正四面体的体积：
| 1 |
| 3 |
| ||
| 4 |
R2-(
|
| ||
| 12 |
故答案为：
| ||
| 12 |
点评：本题考查棱柱、棱锥、棱台的体积，考查学生分析问题解决问题的能力，是基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
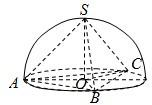在半径为R的球内有一内接正三棱锥，其底面上的三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点返回，则经过的最短路程是
R
R
R
R
R
R
R
R
