题目内容
某地有两所中学,为了检验两校初中毕业生的语文水平,从甲、乙两校九年级学生中各随机抽取20%的学生(即占各自九年级学生总数的20%)进行语文测验.甲校32人,有21人及格;乙校24人,有15人及格.
(1)试根据以上数据完成下列2×2列联表;
(2)判断两所中学初中毕业生的语文水平有无显著差别?
附:
K2=
.
(1)试根据以上数据完成下列2×2列联表;
| 及格 | 不及格 | 合计 | |
| 甲 | |||
| 乙 | |||
| 合计 |
附:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
分析:(1)由题意知按学生考试成绩及格与不及格进行统计,甲班及格人数为21人,乙班及格人数为15,从而做出甲班不及格的人数和乙班不及格的人数,列出表格,填入数据.
(2)根据所给的数据,代入求观测值的公式,做出观测值,把所得的数值同观测值表中的数据进行比较,得到两所中学初中毕业生的语文水平无显著差别.
(2)根据所给的数据,代入求观测值的公式,做出观测值,把所得的数值同观测值表中的数据进行比较,得到两所中学初中毕业生的语文水平无显著差别.
解答:解:(1)
(6分)
(2)k=
=
≈0.058.(10分)
因为k≈0.058<0.455,所以两所中学初中毕业生的语文水平无显著差别.(12分)
| 及格 | 不及格 | 合计 | |
| 甲 | 21 | 11 | 32 |
| 乙 | 15 | 9 | 24 |
| 合计 | 36 | 20 | 56 |
(2)k=
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
| 56(21×9-11×15)2 |
| 32×24×36×20 |
因为k≈0.058<0.455,所以两所中学初中毕业生的语文水平无显著差别.(12分)
点评:本题考查独立性检验的作用,考查列联表的做法,是一个基础题,这种题目运算量比较小,但是需要注意计算观测值时,数据运算比较麻烦,需要认真完成.

练习册系列答案
相关题目
某地有两所中学,为了检验两校初中毕业生的语文水平,从甲、乙两校九年级学生中各随机抽取20%的学生(即占各自九年级学生总数的20%)进行语文测验.甲校32人,有21人及格;乙校24人,有15人及格.
(1)试根据以上数据完成下列2×2列联表;
(2)判断两所中学初中毕业生的语文水平有无显著差别?
附:
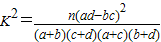 .
.
(1)试根据以上数据完成下列2×2列联表;
| 及格 | 不及格 | 合计 | |
| 甲 | |||
| 乙 | |||
| 合计 |
附:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
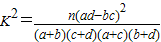 .
.
某地有两所中学,为了检验两校初中毕业生的语文水平,从甲、乙两校九年级学生中各随机抽取20%的学生(即占各自九年级学生总数的20%)进行语文测验.甲校32人,有21人及格;乙校24人,有15人及格.
(1)试根据以上数据完成下列2×2列联表;
(2)判断两所中学初中毕业生的语文水平有无显著差别?
附:
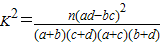 .
.
(1)试根据以上数据完成下列2×2列联表;
| 及格 | 不及格 | 合计 | |
| 甲 | |||
| 乙 | |||
| 合计 |
附:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
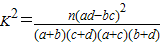 .
.