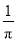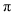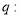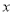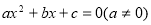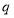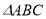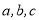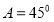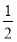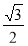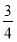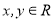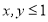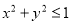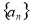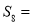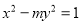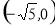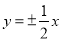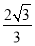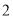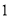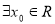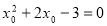Question

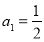已知数列，，且满足．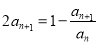

（1）求证数列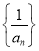是等差数列；

（2）设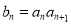，求数列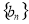的前ｎ项和．

 

Answer 1

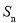（1）参考解析；（2）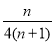

【解析】

试题分析：（1）因为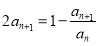，根据这个等式的特点，去分母然后等式的两边同除以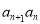.即可得到一个数列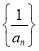是等差数列.本小题的关键是通过要证的结论，从而想到需要构造一个每项的倒数形式的数列.

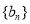（2）通过（1）可得到数列的通项，所以可求出数列的通项，从而通过裂项相减法求得数列的前n项和.

试题解析：（1）因为两边同除以得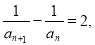

所以数列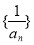是等差数列. 4分

（2） 因为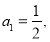所以

所以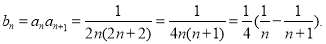

所以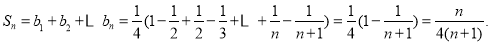 12分[来

考点：1.数列的恒等变形.2.数列的裂项求和的形式.