题目内容
13.过圆x2+y2=5上一点(-1,2)的圆的切线方程是x-2y+5=0.分析 求出圆心与已知点确定直线的斜率,利用两直线垂直时斜率的乘积为-1求出过此点切线方程的斜率,即可求出切线方程.
解答 解:由圆x2+y2=5,得到圆心A的坐标为(0,0),
∴连接圆心与点(-1,2)所得直线的斜率为k=-2,
∴过圆x2+y2=5上一点(-1,2)的圆的切线的斜率为$\frac{1}{2}$,
则切线方程为y-2=$\frac{1}{2}$(x+1),
整理得:x-2y+5=0.
故答案为:x-2y+5=0.
点评 本题考查了直线与圆的位置关系,涉及的知识有:两直线垂直时斜率满足的关系,以及直线的点斜式方程,找出切线的斜率是解本题的关键,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
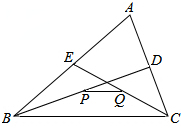

| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |