题目内容
二项式(4x-2-x)6(x∈R)展开式中的常数项是 .
【答案】分析:利用二项展开式的通项公式Tr+1=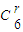 •(4x)6-r•(-1)r•(2-x)r,令2的指数次幂为0即可求得答案.
•(4x)6-r•(-1)r•(2-x)r,令2的指数次幂为0即可求得答案.
解答:解:设二项式(4x-2-x)6(x∈R)展开式的通项公式为Tr+1,
则Tr+1=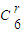 •(4x)6-r•(-1)r•(2-x)r
•(4x)6-r•(-1)r•(2-x)r
=(-1)r• •212x-3rx,
•212x-3rx,
∵x不恒为0,令12x-3rx=0,
则r=4.
∴展开式中的常数项是(-1)4•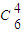 =
= =15.
=15.
故答案为:15.
点评:本题考查二项展开式的通项公式,求得r=4是关键,也是难点所在,属于中档题.
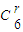 •(4x)6-r•(-1)r•(2-x)r,令2的指数次幂为0即可求得答案.
•(4x)6-r•(-1)r•(2-x)r,令2的指数次幂为0即可求得答案.解答:解:设二项式(4x-2-x)6(x∈R)展开式的通项公式为Tr+1,
则Tr+1=
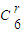 •(4x)6-r•(-1)r•(2-x)r
•(4x)6-r•(-1)r•(2-x)r=(-1)r•
 •212x-3rx,
•212x-3rx,∵x不恒为0,令12x-3rx=0,
则r=4.
∴展开式中的常数项是(-1)4•
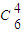 =
= =15.
=15.故答案为:15.
点评:本题考查二项展开式的通项公式,求得r=4是关键,也是难点所在,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目