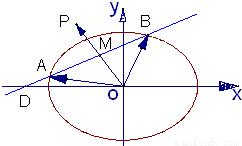
题目内容
如图,已知过点D(-2,0)的直线l与椭圆
(1)若![]() =
=![]() +
+![]() ,求点P的轨迹方程;
,求点P的轨迹方程;
(2)求![]() 的取值范围.
的取值范围.
解:(1)设直线l的方程为y=k(x+2),P(x,y),A(x1,y1),B(x2,y2),
由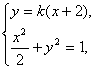 得(1+2k2)x2+8k2x+8k2-2=0.
得(1+2k2)x2+8k2x+8k2-2=0.
∴Δ=64k4-4(1+2k2)(8k2-2)>0.∴0≤k2<![]() .
.
∵![]() =
=![]() +
+![]() ,
,
∴x=x1+x2=-![]() ,y=y1+y2=k(x1+x2+4)=
,y=y1+y2=k(x1+x2+4)=![]() ,
,
消去k,得x2+2y2+4x=0.
又x=-![]() =-4+
=-4+![]() ∈(-2,0],
∈(-2,0],
∴点P的轨迹方程为x2+2y2+4x=0(-2<x≤0).
(2)![]() =
=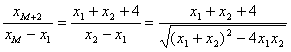
=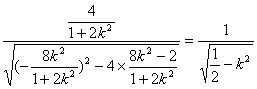 .
.
∵0≤k2<![]() ,∴
,∴![]() ∈[
∈[![]() ,+∞).
,+∞).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
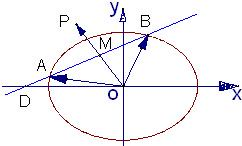 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆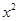 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.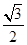 的椭圆
的椭圆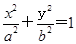 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
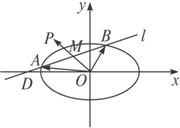
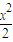 +y2=1交于不同的两点A、B,点M是弦AB的中点
+y2=1交于不同的两点A、B,点M是弦AB的中点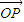 =
=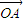 +
+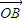 ,求点P的轨迹方程;
,求点P的轨迹方程;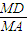 |的取值范围
|的取值范围