题目内容
23、在矩形纸片内取n(n∈N*)个点,连同矩形的4个顶点共(n+4)个点,这(n+4)个点中无三点同在一直线上,以这些点作三角形的顶点,把矩形纸片剪成若干个三角形纸片,把这些三角形纸片的个数记为an.
(1)求a1,a2.
(2)求数列{an}的递推公式.
(3)根据递推公式写出数列{an}的前6项.
(1)求a1,a2.
(2)求数列{an}的递推公式.
(3)根据递推公式写出数列{an}的前6项.
分析:(1)由题意知a1=4,a2=6.
(2)由题意可知每增加1个点Ai剪成的三角形纸层实际增加2个,由此可知an=an-1+2(n≥2).
(3) 把n=1,2,3,4,5,6分别代入an=an-1+2(n≥2),可以求出数列{an}的前6项.
(2)由题意可知每增加1个点Ai剪成的三角形纸层实际增加2个,由此可知an=an-1+2(n≥2).
(3) 把n=1,2,3,4,5,6分别代入an=an-1+2(n≥2),可以求出数列{an}的前6项.
解答: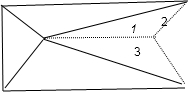 解:(1)a1=4,a2=6
解:(1)a1=4,a2=6
(2)因为这n+4个点中无三点共线,所以每增加1个点Ai(如图,点Ai必在某一个三角形内)剪成的三角形纸层新增3个(图中的1,2,3)但减少了原来的1个,实际增加2个,所以的递推公式是an=an-1+2(n≥2).
(3) a1=4,a2=a1+2=4+2=6,
a3=a2+2=6+2=8
a4=a3+2=8+2=10
a5=a4+2=10+2=12
a6=a5+2=12+2=14
 解:(1)a1=4,a2=6
解:(1)a1=4,a2=6(2)因为这n+4个点中无三点共线,所以每增加1个点Ai(如图,点Ai必在某一个三角形内)剪成的三角形纸层新增3个(图中的1,2,3)但减少了原来的1个,实际增加2个,所以的递推公式是an=an-1+2(n≥2).
(3) a1=4,a2=a1+2=4+2=6,
a3=a2+2=6+2=8
a4=a3+2=8+2=10
a5=a4+2=10+2=12
a6=a5+2=12+2=14
点评:本题考查数列的性质和应用,解题时要注意观察分析能力和归纳总结能力的培养.

练习册系列答案
相关题目