题目内容
(22)设函数(Ⅰ)当x=6时,求![]() 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明![]() >
>![]()
(Ⅲ)是否存在![]() ,使得an<
,使得an<![]() <
<![]() 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
本题考察函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法。考查综合推理论证与分析解决问题的能力及创新意识。
(Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是![]()
(Ⅱ)证法一:因![]()
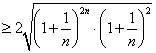
![]()
![]()
![]()
![]()
证法二:
因![]()
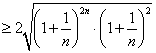
![]()
而![]()
故只需对![]() 和
和![]() 进行比较。
进行比较。
令![]() ,有
,有![]()
由![]() ,得
,得![]()
因为当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增,所以在
单调递增,所以在![]() 处
处![]() 有极小值
有极小值![]()
故当![]() 时,
时,![]() ,
,
从而有![]() ,亦即
,亦即![]()
故有![]() 恒成立。
恒成立。
![]()
![]()
所以![]() ,原不等式成立。
,原不等式成立。
(Ⅲ)对![]() ,且
,且![]()
有![]()
![]()
![]()
![]()
![]()
![]()
![]()
又因![]() ,故
,故![]()
∵![]() ,从而有
,从而有![]() 成立,
成立,
即存在![]() ,使得
,使得![]() 恒成立。
恒成立。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ,其中b≠0.
,其中b≠0.
 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
 都成立.
都成立. .
.
 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
 ;
;
 ,使得
,使得 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.