题目内容
已知集合A= ,B=(2a,a2+1).
,B=(2a,a2+1).
(Ⅰ)当a=2时,求A B;
B;
(Ⅱ)求使B  A的实数a的取值范围.
A的实数a的取值范围.
(Ⅰ)A B=(4,5)(Ⅱ)[1,3]∪{-1}
B=(4,5)(Ⅱ)[1,3]∪{-1}
解析试题分析:(Ⅰ)当a=2时,A=(2,7),B=(4,5),
∴ A B=(4,5).
B=(4,5).
(Ⅱ)∵ B=(2a,a2+1),
当a<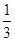 时,A=(3a+1,2),
时,A=(3a+1,2),
要使B  A,必须
A,必须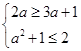 ,此时a=-1;
,此时a=-1;
当a=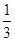 时,A=
时,A=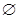 ,
,
使B  A的a不存在;
A的a不存在;
当a>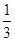 时,A=(2,3a+1),
时,A=(2,3a+1),
要使B  A,必须
A,必须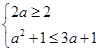 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B  A的实数a的取值范围为[1,3]∪{-1}.
A的实数a的取值范围为[1,3]∪{-1}.
考点:本小题主要考查集合的关系和运算.
点评:求解此小题时,不要忘记对a的范围进行讨论,讨论要做到不重不漏,而且求解不等式组时,可以借助数轴辅助解决问题.

练习册系列答案
相关题目
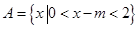 ,
,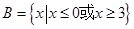 .分别求出满足下列条件的实数
.分别求出满足下列条件的实数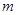 的取值范围.
的取值范围.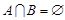 ;
;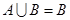 .
. 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .
. ;
; ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。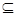 Q,求实数a的取值范围.
Q,求实数a的取值范围. ,已知集合
,已知集合 ,集合
,集合 ,.
,.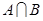 ,
, ;
; ,集合
,集合 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,集合
,集合 ,集合
,集合 .
. ,求
,求 ; (Ⅱ)若
; (Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
 的定义域为集合A,函数
的定义域为集合A,函数
 的定义域为集合B
的定义域为集合B 时,求
时,求
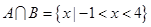 ,求实数
,求实数 的值
的值  ,
, ,
,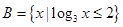 .
. ; (Ⅱ)求
; (Ⅱ)求 .
.