题目内容
已知
，且A中至少有一个奇数，则这样的集合A共有（ ）
| A．11个 | B．12个 | C．15个 | D．16个 |
B
解析试题分析：根据题意，分A中有1个奇数或2个奇数两种情况讨论，由排列组合知识易得每种情况下的集合A数目，由分步计数原理计算可得答案解：根据题意，A中至少有一个奇数，包含两种情况，A中有1个奇数或2个奇数，若A中含1个奇数，有C21×22=8， A中含2个奇数：C22×22=4，由分类计数原理可得．共有8+4=12种情况；故选B．
考点：排列、组合
点评：本题考查排列、组合的运用，解题的关键在于对“A中至少有一个奇数”的理解，进而分“A中有1个奇数或2个奇数”两种情况讨论．
练习册系列答案
相关题目
若集合
A． | B． |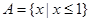
C． | D． |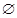
设集合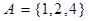
，
，则
等于（ ）
| A．｛２｝ | B．｛１，２，４，６｝ |
| C．｛１，２，４｝ | D．｛２，６｝ |
设集合
，则
（ ）
A． | B． | C． | D． |
集合
若
则
| A．{2,3,4} | B．{2 ,4} | C．{2,3} | D．{1，2,3,4} |
已知集合
,则
等于
A． | B． |
C． | D． |
已知全集
，集合
，
，那么
A． | B． | C． | D． |
已知集合
，
，则
为（ ）
A． | B． | C． | D． |
设集合
，
，则
( )
A． | B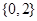． | C． | D． |