题目内容
极坐标方程ρcosθ=2sin2θ表示的曲线为
- A.一条射线和一个圆
- B.两条直线
- C.一条直线和一个圆
- D.一个圆
C
分析:将极坐标方程化为直角坐标方程,就可以得出结论
解答:极坐标方程ρcosθ=2sin2θ可化为:ρcosθ=4sinθcosθ
∴cosθ=0或ρ=4sinθ
∴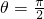 或x2+y2-4y=0
或x2+y2-4y=0
∴极坐标方程ρcosθ=2sin2θ表示的曲线为一条直线和一个圆
故选C.
点评:研究极坐标问题,我们的解法是将极坐标方程化为直角坐标方程,再进行研究.
分析:将极坐标方程化为直角坐标方程,就可以得出结论
解答:极坐标方程ρcosθ=2sin2θ可化为:ρcosθ=4sinθcosθ
∴cosθ=0或ρ=4sinθ
∴
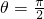 或x2+y2-4y=0
或x2+y2-4y=0∴极坐标方程ρcosθ=2sin2θ表示的曲线为一条直线和一个圆
故选C.
点评:研究极坐标问题,我们的解法是将极坐标方程化为直角坐标方程,再进行研究.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
极坐标方程ρ=cosθ与ρcosθ=
的图形是( )
| 1 |
| 2 |
A、 |
B、 |
C、 |
D、 |