题目内容
16.计算:(1)${log_{\sqrt{2}}}2\sqrt{2}+{log_2}3•{log_3}\frac{1}{2}$=2;(2)设f(x)=$\left\{\begin{array}{l}{2^{x+1}}(x≥0)\\ f(x+1)+2(x<0)\end{array}$,则$f(-\frac{2015}{2})$=$2\sqrt{2}+2016$.
分析 (1)利用对数的运算法则,可得结论;
(2)当x<0时,f(x)=f(x+1)+2,代入计算,即可得出结论.
解答 解:(1)原式=$lo{g}_{\sqrt{2}}(\sqrt{2})^{3}$+$\frac{lg3}{lg2}•\frac{-lg2}{lg3}$=3-1=2;
(2)当x<0时,f(x)=f(x+1)+2,
∴原式=$f(-\frac{2015}{2})$=$f(-1007-\frac{1}{2})$=f(-1006-$\frac{1}{2}$)+2=f(-1005-$\frac{1}{2}$)+2×2=…=f($\frac{1}{2}$)+2×1008=$2\sqrt{2}+2016$
故答案为:2;$2\sqrt{2}+2016$.
点评 本题考查了指数幂与对数的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设函数f(x)=x(ex-e-x),则使得f(x)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
8.已知数列{an}为等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为$\frac{5}{4}$,则S6=( )
| A. | 35 | B. | 33 | C. | 31 | D. | $\frac{63}{2}$ |
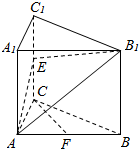 已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.
已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.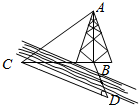 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.