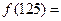题目内容
(本题满分12分)已知函数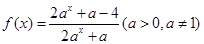 是定义在R上的奇函数.
是定义在R上的奇函数.
(I)求实数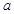 的值;
的值;
(II)判断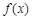 在定义域上的单调性,并用单调性定义证明;
在定义域上的单调性,并用单调性定义证明;
(III)当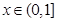 时,
时,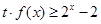 恒成立,求实数
恒成立,求实数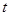 的取值范围.
的取值范围.
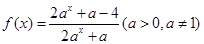 是定义在R上的奇函数.
是定义在R上的奇函数.(I)求实数
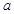 的值;
的值;(II)判断
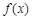 在定义域上的单调性,并用单调性定义证明;
在定义域上的单调性,并用单调性定义证明;(III)当
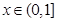 时,
时,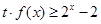 恒成立,求实数
恒成立,求实数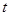 的取值范围.
的取值范围. 证明:任取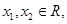 且
且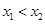
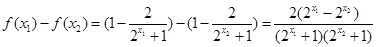 5分
5分
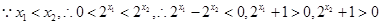
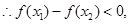 即
即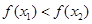 所以
所以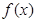 是R上
是R上 的增函数. 7分
的增函数. 7分
(III)不等式: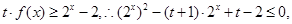
令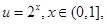 则
则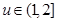 .
.
于是,当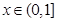 时,
时,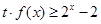 恒成立,
恒成立,
即:当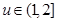 时,
时,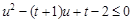 恒成立; 9分
恒成立; 9分
方法一:令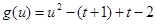
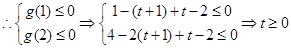
所以实数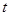 的取值范围是
的取值范围是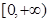 . 12分
. 12分
方法二:
令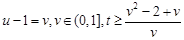 ,而
,而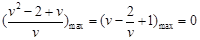 ,所以
,所以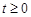 . 12分
. 12分
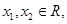 且
且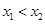
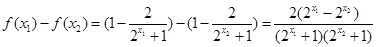 5分
5分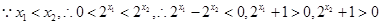
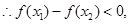 即
即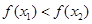 所以
所以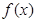 是R上
是R上 的增函数. 7分
的增函数. 7分(III)不等式:
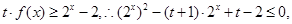
令
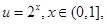 则
则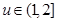 .
.于是,当
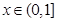 时,
时,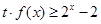 恒成立,
恒成立,即:当
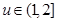 时,
时,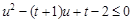 恒成立; 9分
恒成立; 9分方法一:令
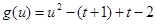
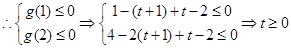
所以实数
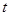 的取值范围是
的取值范围是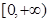 . 12分
. 12分方法二:

令
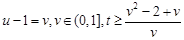 ,而
,而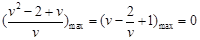 ,所以
,所以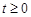 . 12分
. 12分略

练习册系列答案
相关题目
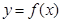 的图像与函数
的图像与函数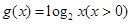 的图像关于原点对称,则
的图像关于原点对称,则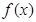 的表达式为
的表达式为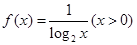
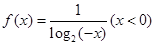
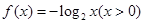
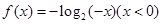
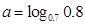 ,
,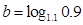 ,
,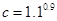 ,那么( )
,那么( )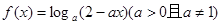 在区间(0,
在区间(0,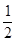 )上是减函数,则实数a 的取值范围
)上是减函数,则实数a 的取值范围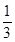 ,现在价格为8100元的计算机,9年后的价格可降为___________元.
,现在价格为8100元的计算机,9年后的价格可降为___________元.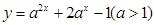 在区间[-1,1]上的最大值是14,求a的值.
在区间[-1,1]上的最大值是14,求a的值.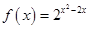 在区间
在区间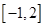 上的值域是__________________.
上的值域是__________________.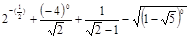 ,结果是( )
,结果是( )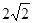
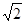
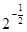
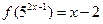 ,则
,则