题目内容
已知一条不在y轴左侧的曲线E上的每个点到A(1,0)的距离减去它到y轴的距离差都是1.
(1)求曲线E的方程;
(2)已知曲线E的一条焦点弦被焦点分成长为m、n两部分,试判断
+
是否为定值,若是求出定值并加以证明,若不是,请说明理由.
(1)求曲线E的方程;
(2)已知曲线E的一条焦点弦被焦点分成长为m、n两部分,试判断
| 1 |
| m |
| 1 |
| n |
分析:(1)由题意及抛物线的定义可判断曲线E为以点A为焦点的抛物线,从而可得其方程;
(2)几何法:当焦点垂直x轴时易求
+
的值;当焦点不垂直x轴时,作出示意图,利用抛物线定义及三角形相似可得m,n间的关系式,化简后整理即可得到
+
的值,综上可得结论.
(2)几何法:当焦点垂直x轴时易求
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
解答:解:(1)由曲线E上的每个点到A(1,0)的距离减去它到y轴的距离差都是1,知曲线E上的点到A的距离等于到x=-1的距离,
所以曲线E为以A为焦点、x=-1为准线的抛物线,
所以曲线E的方程为:y2=4x;
(2)
+
是定值为1,证明如下:
当焦点弦垂直x轴时,把x=-1代入抛物线方程y2=4x,得y═±2,
所以此时m=n=2,故
+
=
+
=1;
当焦点弦不垂直x轴时,如下图所示:
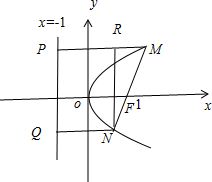
不妨设MF=m,NF=n,且m>n,则PM=m,QN=n,设NR交x轴与S,则SF=2-n,RM=m-n,
在Rt△MNR中,由三角形相似得
=
,即
=
,即(2-n)(m+n)=n(m-n),
所以(m+n)=mn,两边同除以mn得
+
=1,即为定值1.
综上,
+
为定值1.
所以曲线E为以A为焦点、x=-1为准线的抛物线,
所以曲线E的方程为:y2=4x;
(2)
| 1 |
| m |
| 1 |
| n |
当焦点弦垂直x轴时,把x=-1代入抛物线方程y2=4x,得y═±2,
所以此时m=n=2,故
| 1 |
| m |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
当焦点弦不垂直x轴时,如下图所示:
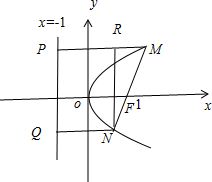
不妨设MF=m,NF=n,且m>n,则PM=m,QN=n,设NR交x轴与S,则SF=2-n,RM=m-n,
在Rt△MNR中,由三角形相似得
| SF |
| RM |
| NF |
| NM |
| 2-n |
| m-n |
| n |
| m+n |
所以(m+n)=mn,两边同除以mn得
| 1 |
| m |
| 1 |
| n |
综上,
| 1 |
| m |
| 1 |
| n |
点评:本题考查函数与方程的综合运用,考查抛物线的定义及直线与圆锥曲线的位置关系,要认真体会几何图形在本题中的应用.

练习册系列答案
相关题目
 是否为定值,若是求出定值并加以证明,若不是,请说明理由.
是否为定值,若是求出定值并加以证明,若不是,请说明理由.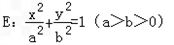 上,设椭圆E与y轴正半轴的交点为B,其左焦点为F,且∠AFB=150°.
上,设椭圆E与y轴正半轴的交点为B,其左焦点为F,且∠AFB=150°.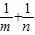 是否为定值,若是求出定值并加以证明,若不是,请说明理由.
是否为定值,若是求出定值并加以证明,若不是,请说明理由.